Thomas Auzinger, Michael Guthe, Stefan Jeschke
Analytic Anti-Aliasing of Linear Functions on Polytopes
Computer Graphics Forum (Proceedings of EUROGRAPHICS 2012), 31(2):335-344, May 2012. [Paper]

Information

  • Publication Type: Journal Paper with Conference Talk
  • Workgroup(s)/Project(s):
  • Date: May 2012
  • Journal: Computer Graphics Forum (Proceedings of EUROGRAPHICS 2012)
  • Volume: 31
  • Number: 2
  • Location: Cagliari, Italy
  • Lecturer: Thomas Auzinger
  • Event: Eurographics 2012
  • Conference date: 13. May 2012 – 18. May 2012
  • Pages: 335 – 344
  • Keywords: Polytope, Filter Design, Analytic Anti-Aliasing, Sampling, Integral Formula, Spherically Symmetric Filter, CUDA, Closed Form Solution, 2D 3D

Abstract

This paper presents an analytic formulation for anti-aliased sampling of 2D polygons and 3D polyhedra. Our framework allows the exact evaluation of the convolution integral with a linear function defined on the polytopes. The filter is a spherically symmetric polynomial of any order, supporting approximations to refined variants such as the Mitchell-Netravali filter family. This enables high-quality rasterization of triangles and tetrahedra with linearly interpolated vertex values to regular and non-regular grids. A closed form solution of the convolution is presented and an efficient implementation on the GPU using DirectX and CUDA C is described.

Additional Files and Images

Additional images and videos

Fast Forward DivX: Video for the Fast Forward session (DivX encoded) (14 MB). Fast Forward DivX: Video for the Fast Forward session (DivX encoded) (14 MB).
Fast Forward TechSmith: Video for the Fast Forward session (TechSmith encoded) (107 MB). Fast Forward TechSmith: Video for the Fast Forward session (TechSmith encoded) (107 MB).
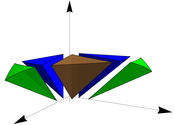Intersection decomposition: Decomposition of the intersection volume between the spherical filter support and a input tetrahedron. The different colors denote different geometrical shapes for which a closed form solution of the integral can be obtained. Intersection decomposition: Decomposition of the intersection volume between the spherical filter support and a input tetrahedron. The different colors denote different geometrical shapes for which a closed form solution of the integral can be obtained.
Sea urchin model: Volume rendering of a sea urchin model sampled with our method. The color is linearly interpolated in the spike tetrahedra. The model consists of 2470 tetrahedra and is sampled to a grid with resolution 256³ with a Gaussian filter kernel of radius 2.3 voxels. Sea urchin model: Volume rendering of a sea urchin model sampled with our method. The color is linearly interpolated in the spike tetrahedra. The model consists of 2470 tetrahedra and is sampled to a grid with resolution 256³ with a Gaussian filter kernel of radius 2.3 voxels.
Zone plate model: Volume rendering of a zone plate model consisting of 2M tetrahedra with a Gaussian filter kernel. Zone plate model: Volume rendering of a zone plate model consisting of 2M tetrahedra with a Gaussian filter kernel.
sea_urchin_thumbnail
sea_urchin_thumbnail

Additional files

Paper: Full paper preprint. Paper: Full paper preprint.
Slides: Presentation slides without the final video (5 MB). Slides: Presentation slides without the final video (5 MB).
SlidesVideo: Presentation slides with the final video (20 MB). SlidesVideo: Presentation slides with the final video (20 MB).

Weblinks

BibTeX

@article{Auzinger_2012_AAA,
  title =      "Analytic Anti-Aliasing of Linear Functions on Polytopes",
  author =     "Thomas Auzinger and Michael Guthe and Stefan Jeschke",
  year =       "2012",
  abstract =   "This paper presents an analytic formulation for anti-aliased
               sampling of 2D polygons and 3D polyhedra. Our framework
               allows the exact evaluation of the convolution integral with
               a linear function defined on the polytopes. The filter is a
               spherically symmetric polynomial of any order, supporting
               approximations to refined variants such as the
               Mitchell-Netravali filter family. This enables high-quality
               rasterization of triangles and tetrahedra with linearly
               interpolated vertex values to regular and non-regular grids.
               A closed form solution of the convolution is presented and
               an efficient implementation on the GPU using DirectX and
               CUDA C is described.",
  month =      may,
  journal =    "Computer Graphics Forum (Proceedings of EUROGRAPHICS 2012)",
  volume =     "31",
  number =     "2",
  pages =      "335--344",
  keywords =   "Polytope, Filter Design, Analytic Anti-Aliasing, Sampling,
               Integral Formula, Spherically Symmetric Filter, CUDA, Closed
               Form Solution, 2D 3D",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2012/Auzinger_2012_AAA/",
}