Volume Visualization Renderer

Dokumentation

Algorithmus

Einleitung

Um Direct Volume Rendering Durchzuführen braucht man einen dreidimensionalen Datensatz mit Voxelwerten. Solche Datensätze erhält man zum Beispiel von Computertomographen. In unserem Fall konnten wir davon ausgehen, dass dieser Datensatz auch schon so weit bearbeitet ist um in direkt zu rendern. Man hatte also einen Array der Form: V[x][y][z]. Jeder dieser Voxelwerte entspricht der Dichte des Materials an dieser Stelle (x, y, z).

Der eigentliche Algorithmus von Levoy funktioniert dann so, dass man einen Ray aus der Richtung des Betrachters (Kamera) in die Datenwolke schießt. In gewissen regelmäßigen Abständen werden dabei Samples genommen.

In der Regel stimmt die Position von Samplepoints nicht genau mit denen der Voxelwerte überein. In solchen Fällen gibt es zwei Möglichkeiten: erstens kann der am nähesten liegende Voxelwert (nearest Neighbor) für die weitere Berechnung verwendet werden oder zweitens, man macht eine trilineare Interpolation zwischen den acht Voxelwerten, welche den Samplepoint umgeben.

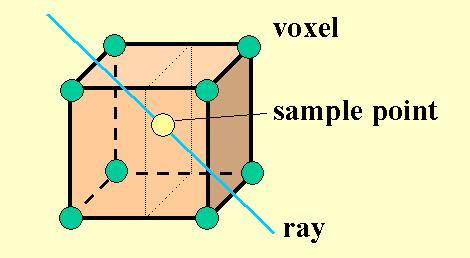
In dem von uns erstellten Programm kann man sich aussuchen welche der beiden Arten der Wertegewinnung man verwenden will. Wie man sich leicht vorstellen kann ist die Methode der trilinearen Interpolation feiner als die Methode des nearest Neighbors, jedoch ist diese Methode auch langsamer.

Im den folgenden Punkten wird jetzt erklärt wie man die Farbwerte und die Durchsichtigkeit der Voxel berechnet. Diese Werte werden danach zur Interpolation auf die gesuchten Werte der Samplepoints verwendet.

Berechnung der Farbwerte der Voxel

Zur Berechnung der Farbwerte wird die Phong Schattierung eingesetzt. Es ist eine auf Beobachtungen basierendes Modell welches sich aber gut eignet um ein brauchbares Ergebnis mit erträglichem Aufwand zu erhalten. Jeder Farbwert setzt sich bei diesem Modell aus drei Komponenten zusammen:

Cr,g,b[x][y][z] = ambient + diffuse + specular

Das Umgebungslicht ambient ergibt sich aus dem Produkt der Intensität des Umgebungslichts (Ia) und eines Reflexionskoeffizienten für ambientes Licht Ka:

ambient = Ia·Ka

Die diffuse Reflektion ergibt sich aus dem Produkt von Lichtquellen-Intensität Il, Reflexionsfaktor Kd und skalarem Produkt der Oberflächennormale N sowie der Richtung der Lichtquelle L:

diffuse = Il·Kd·(N[x][y][z]·L)

Die spekulare Reflexion ergibt sich aus dem Produkt von Lichtquellen-Intensität I, Reflexionsfaktor Ks und skalarem Produkt der Oberflächennormale N sowie der Richtung der maximalen Reflexion H:

specular = Il·Ks·(N[x][y][z]·H), wobei H = (L+V)/2 (V ist der normalisierte Blickvektor)

Die Oberflächennormale N[x][y][z] ist durch den normalisierten Gradientenvektor g[x][y][z] gegeben und kann wie folgt approximiert werden:

				(V[x+1][y][z]-V[x-1][y][z])/2,
				g[x][y][z] = { (V[x][y+1][z]-V[x][y-1][z])/2, }
				(V[x][y][z+1]-V[x][y][z-1])/2
			

Zusammengefasst ergibt sich also:

Cr,g,b[x][y][z] = Ia·Ka + Il ·[Kd·(g[x][y][z]·L) + Ks·(g[x][y][z]·H)]

Berechnung der Transparenzwerte der Voxel

Um für region boundary surfaces passende Transparenzwerte α[x][y][z], benötigt man eine Zuordnung von Voxelwerten Vi zu Transparenzwerten αi. Nach dem Paper von Levoy erfolgt dies nach folgender Funktion:

α[x][y][z] = |g[x][y][z]| · { αi+1·[(V[x][y][z]-Vi)/(Vi+1-Vi)] + αi·[(Vi+1-V[x][y][z])/(Vi+1-Vi)] }
(wenn Vi ≤ V[x][y][z] ≤ Vi+1, 0 sonst)

Wie man in dieser Funktion sieht hängt die Transparenz stark vom Gradienten (g[x][y][z]) vom jeweiligen Voxel ab. Diese Abhängigkeit hat den Sinn, dass man in Volumsdaten vorallem die Übergänge zwischen verschiedenen Materialien besser erkennen kann (für genauere Erkläungen verweisen wir an dieser Stelle auf das Paper von Levoy).

Berechnung des Bildes

Für jeden Bildpunkt P[x][y] wird ein Ray (Blickstrahl) durch die Arrays der Farbwerte C[x][y][z] sowie der Transparenzwerte V[x][y][z] gelegt. Für jeden Samplepunkt entlang des Rays wird dann wie vorher erklärt entweder eine trilineare Interpolation gemacht oder der am nähesten liegende Nachbar verwendet. Die Farbe des Bildpunkts P[x][y] resultiert dann aus einer Kombination der Farbe und Transparenz der betreffenden Voxel:

P[x][y] = ∑z=0,…,Z [ C[x][y][z]·α[x][y][z] · ∏z1=z+1,…,Z (1-α[x][y][z1]) ]
wobei C[x][y][0] = B (B ist die Hintergrundfarbe) und α[x][y][0] = 1.

GUI Dokumentation

Programmstart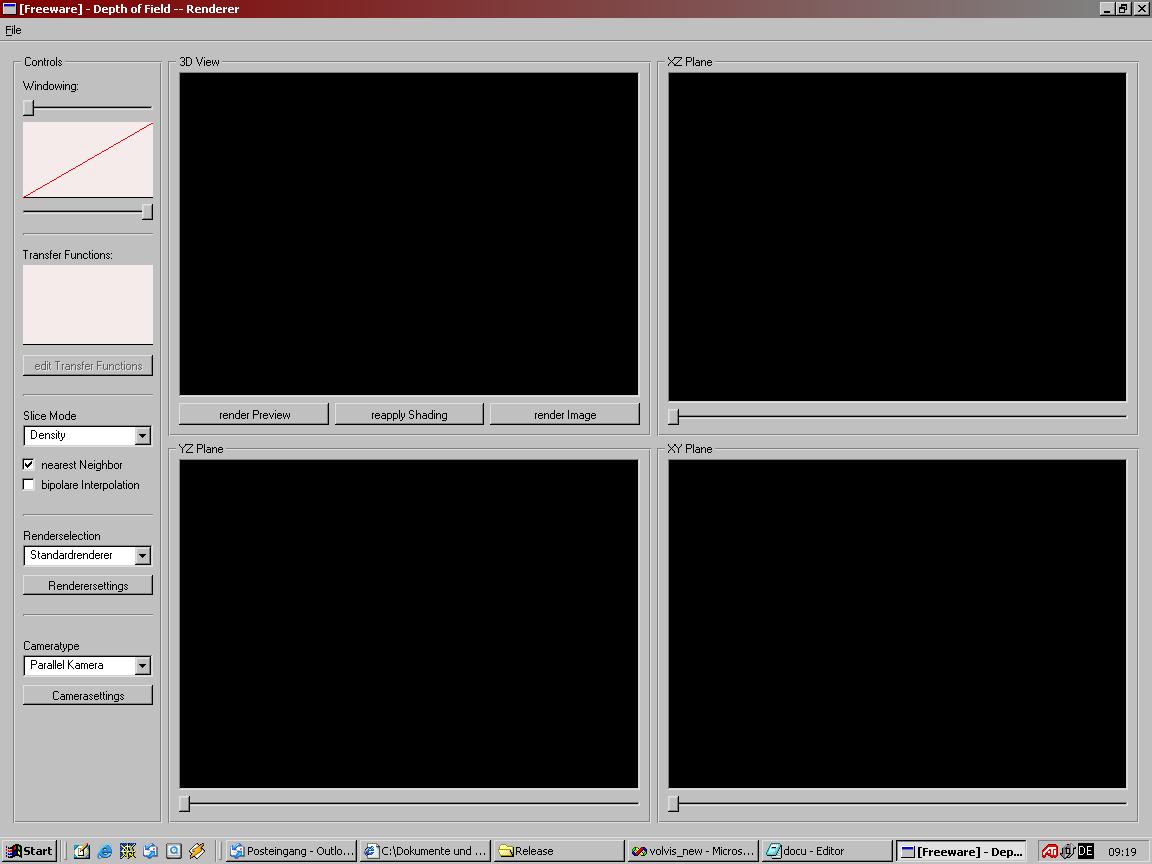

Im ersten Screenshot sieht man das Programm nach dem Starten. Es wurde noch kein Datensatz geladen. Man sieht, dass es vier Hauptfenster gibt. Drei dieser Anzeigefenster dienen der Darstellung der Slices in den drei Hauptachsen. Das vierte Fenster (links oben) dient der Darstellung der gerenderten Volumsdaten. Es soll aber nur aine Vorschau auf das eigentlich Ergebnis bilden. Im linken Bereich des Programms sind die Controlls. In den betreffenden Unterpunkten der weiteren Dokumentation werden die verschiedenen Bedienelemente noch genauer erklärt.

Laden von Daten

Das Programm kann Dateien des Types *.dat laden. Bei diesen Dateien handelt es ich um Raw Dateien. Ein Voxelwert wird in zwei Byte gespeichert. In den ersten sechs Bytes des Files ist die Dimesnion des Datensatzes gespeichert. Die Voxelwerte sind nach den Slices in z-Richtung im File angeordnet. Über den Menüpunkt File->Open kommt man zu folgendem File Dialog:

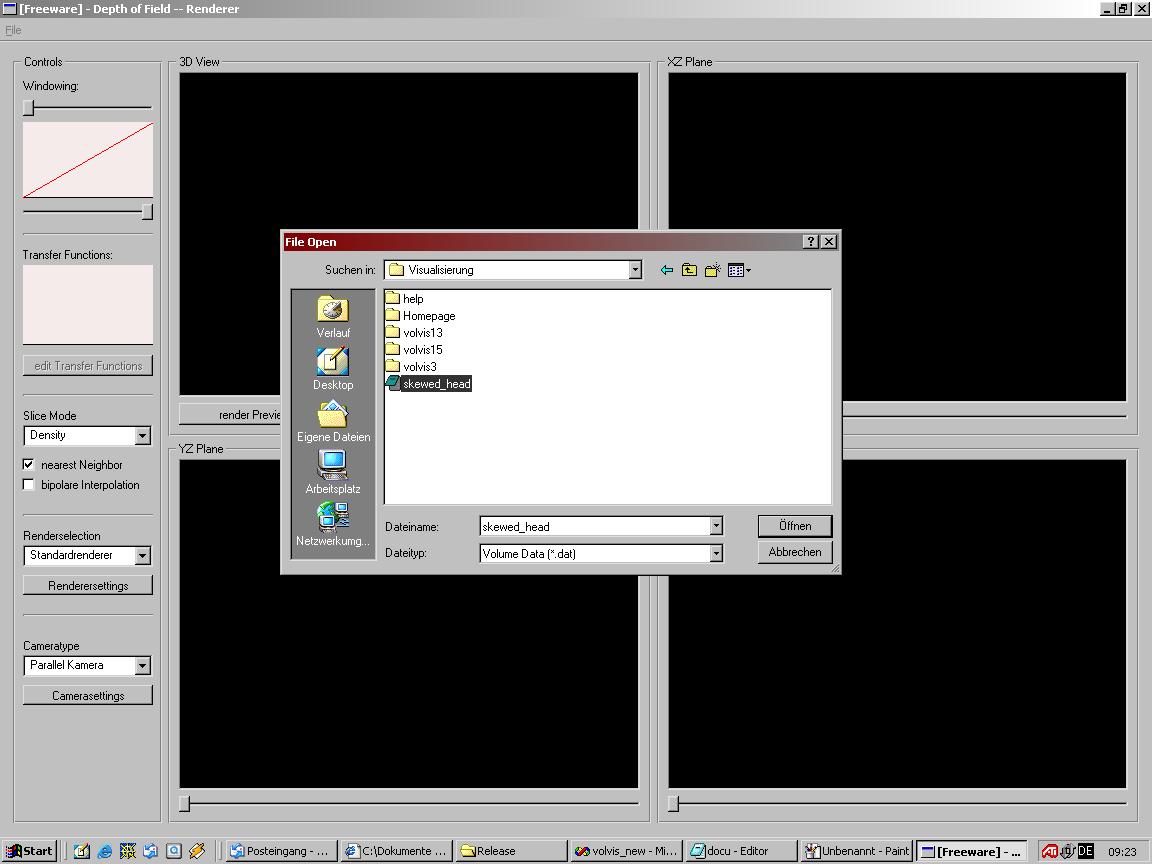
Hat man eine Datei ausgewählt und drückt man auf Open dann beginnt das Preprocessing. Dabei werden die Voxelwerte eingelesen und für jeden Voxelwert der Gradient und damit das Shading berechnet. Für die Berechnung des Shadings der einzelnen Voxelwerte braucht man die Rcihtung der Lichtquelle und die Werte der Koeffizienten für die Mischung aus ambientem, diffusem und spekularem Lichtanteilen an den Voxeln. daher erscheint während des Ladens folgender Dialog:

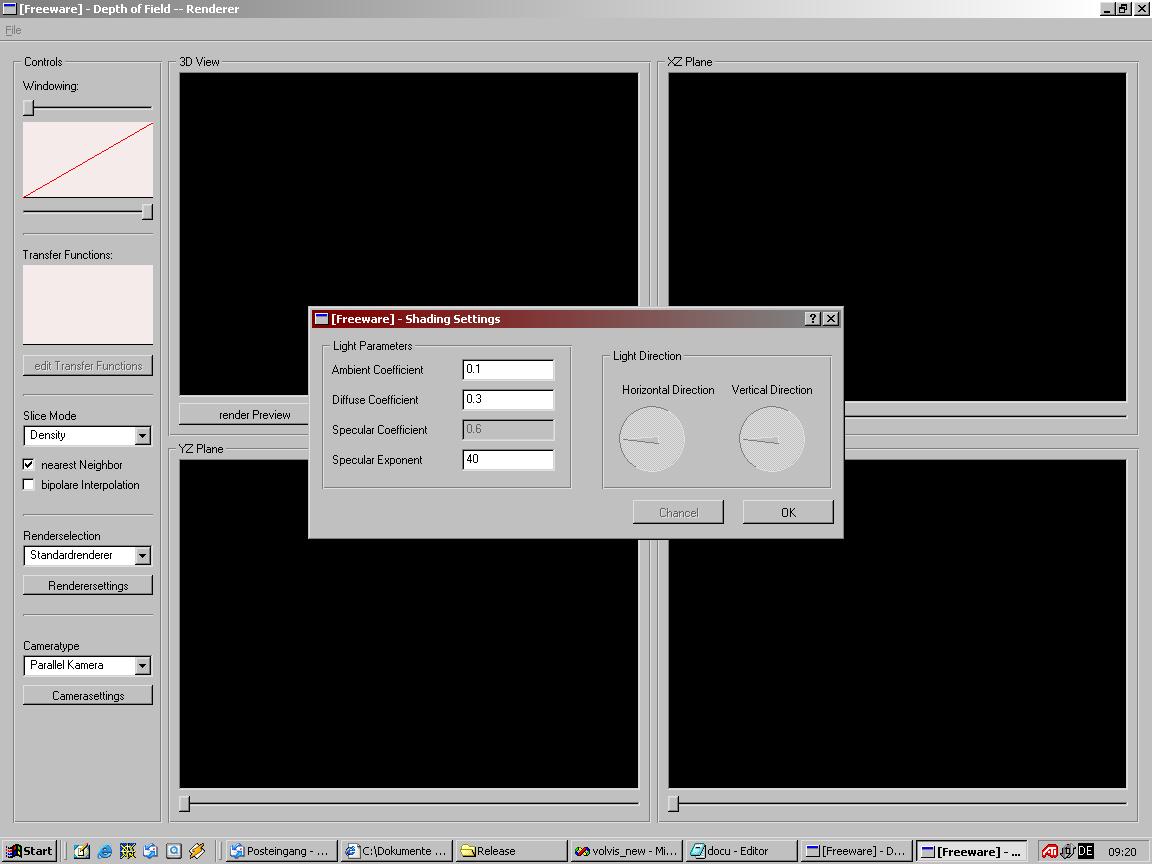
Transfer Function Editor

Ist nun eine Datei geladen, so kann man eine Transfer Function einstellen. Dies erfolgt mit dem Transfer Function Editor. Im Controlls - Bereich des Programms (links) sieht man unter dem namen "Transfer Functions" einen Bereich in dem das Histogram des Datensatzes dargestellt ist. Darunter ist ein Button. Wenn man diesen betätigt kommt man in folgendes Fenster:

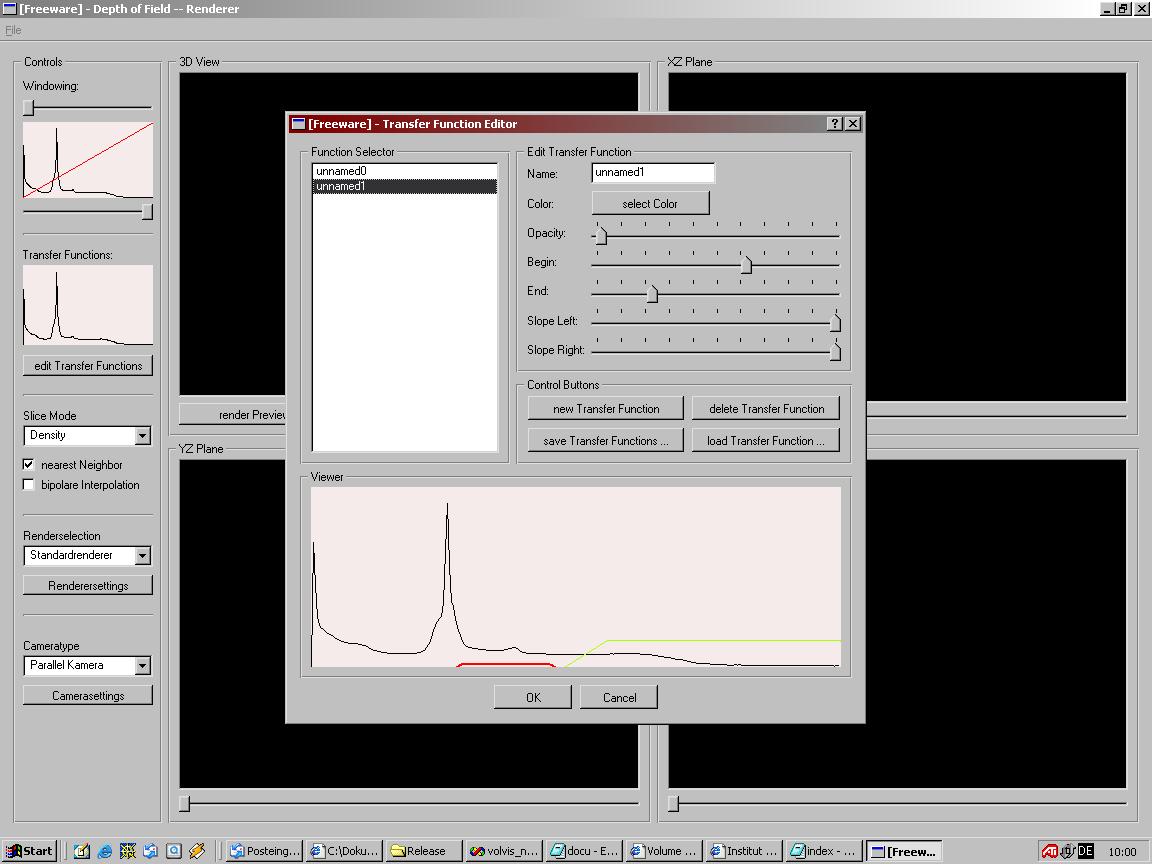
Die Einstellung der Transfer Functions erfolgt mittels der Slider. Für jeden relevanten Wert der Transfer Function gibt es einen eigenen Slider. Mit einem Farbdialog kann jeder Transfer Function ein beliebiger Farbwert zugewiesen werden. Die Controll Buttons sind da um neue Transfer Functions zu erstellen und um welche zu löschen. Es gibt auch die Möglichkeit Files mit Transfer Functions zu laden oder erstellte Transfer Functions in einem File zu speichern.

Wenn man mit dem editieren der Transfer Functions fertig ist, bestätigt man die Änderungen mit dem OK Button. Dies schließt den Editor und übergibt die neuen Transfer Functions an das Hauptfenster. Die geänderten Transfer Functions sieht man auch im Controlls-Bereich des Hauptfensters, wo die aktuellen Einstellungen in der Transfer Function Preview aufscheinen.

Slices

Die Slices werden in den drei Hauptachsrichtungen dargestellt. Unter jedem Anzeigefenster einer Hauptrichtung gibt es einen Slider, mit welchem man die jeweilige Slice-Position in der jeweiligen Richtung einstellen kann. Im Controlls Bereich kann man sich einen Modus aussuchen, wie die Slices gerendert werden sollen:

Es gibt die Renderarten Density, Shading, Transfer Functions und Gradienten. Für die Renderart Density gibt es noch zusätzlich die Möglichkeit einen "Windowing" Bereich einzustellen. Dies führt dazu, dass nicht der gesamte Wertebereich dargestellt wird, sondern nur ein kleinerer ausgewählter Bereich der dann auf den gesamten Wertebereich ausgedehnt wird.

Unter dem Pop-Up Menü sind noch zwei Checkboxes, mit denen man sich die Interpolationsart beim Slice-Rendering aussuchen kann.

Kamera

In unserem Programm gibt es die Möglichkeit zwischen zwei Kameras zu wählen. Zum einen die parallele Kamera und zum anderen die perspektivische Kamera. Die Richtung in welche die Kamera auf die Szene schaut kann man in den Slices einstellen. Denn Fokuspunkt setzt man dabei mit der linken Maustaste und die Richtung des Viewing Vektors mit der rechten Maustaste.

Für jeden Kameratypen gibt es noch weitere Parameter, wie zum Beispiel den Abstand zum Objekt. Diese Parameter kann man in einem Dialog setzen. Dieser erscheint wenn man auf den Button unter dem Kameramode drückt.

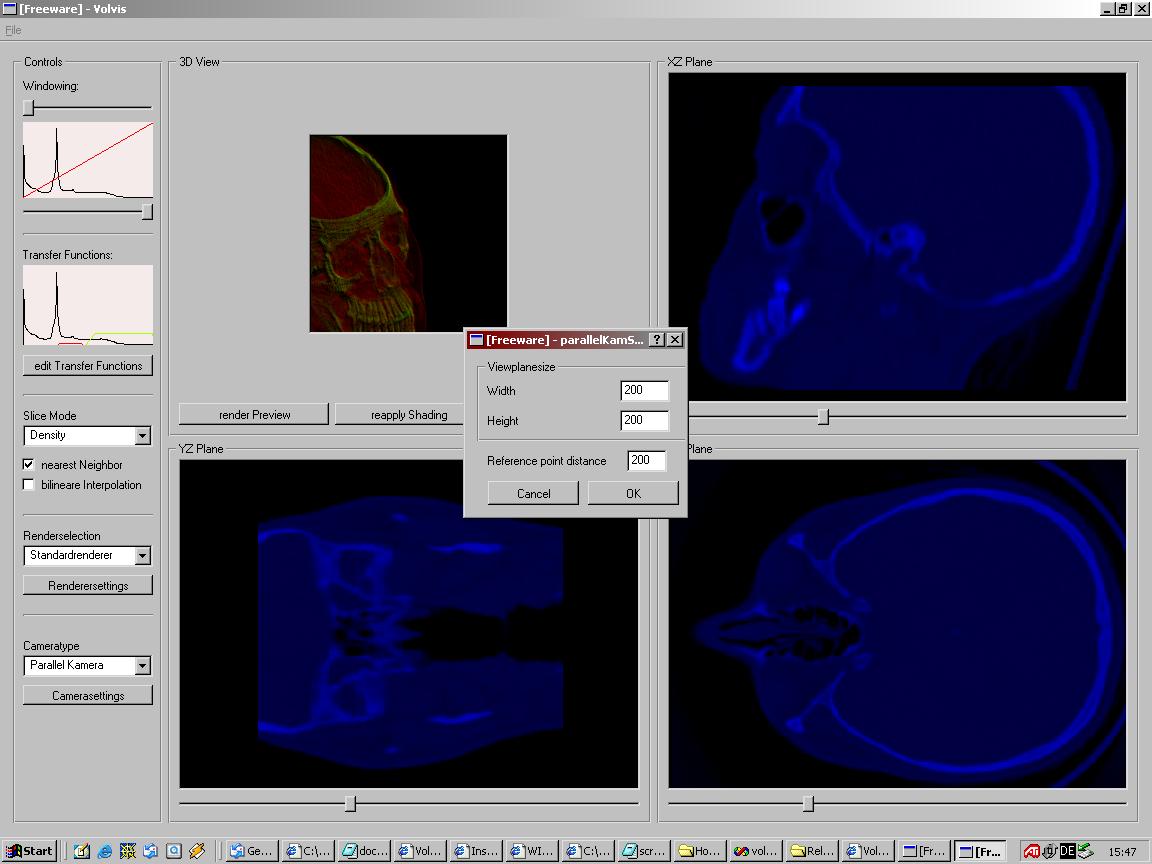
Volume Rendering

Die Hauptaufgabe unseres Programms besteht im Volume Rendering. In unserem Fall gibt es beim Volume Rendering zurzeit zwei Möglichkeiten: "normales" Rendern und High Quality Rendering. High Quality Rendering rendert mit einer Vorbestimmten hohen Auflösung. Das "normale" Rendering hat ein paar Optionen welche man in einem Dialog einstellen kann. Dieser Dialog erscheint wenn man unter den Render Mode Pop-Up auf den Button klickt.

Das eigentliche Rendern erfolgt danach indem die Buttons unter dem Rendering View (linkes oberes Fenster) gedrückt werden. Die Preview erzeugt ein kleines Bild (150*150) und dient wie der Name schon sagt als Preview. Wenn man Render Image drückt, kommt noch ein Dialog in welchem man die Auflösung und den Filter (Trilinear, nearest Neighbor) für den Renderingvorgang angibt.

Bestätigt man diesen Dialog mit dem OK Button, so beginnt das Rendern. Der Rendering Vortschritt wird wie beim Laden und Shaden mit einer Progress Bar angezeigt.

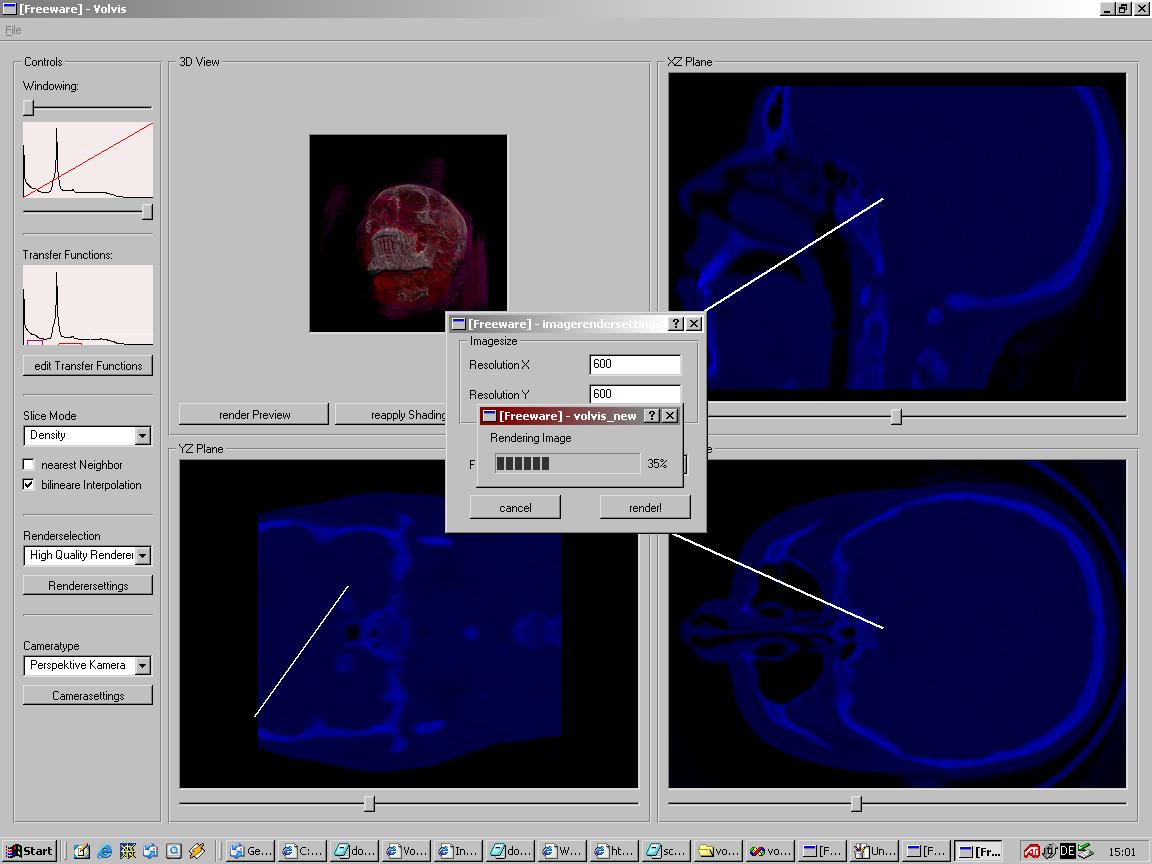
Wenn das Rendering abgeschlossen ist, bekommt man das Ergebnis in einem neuen Fenster.
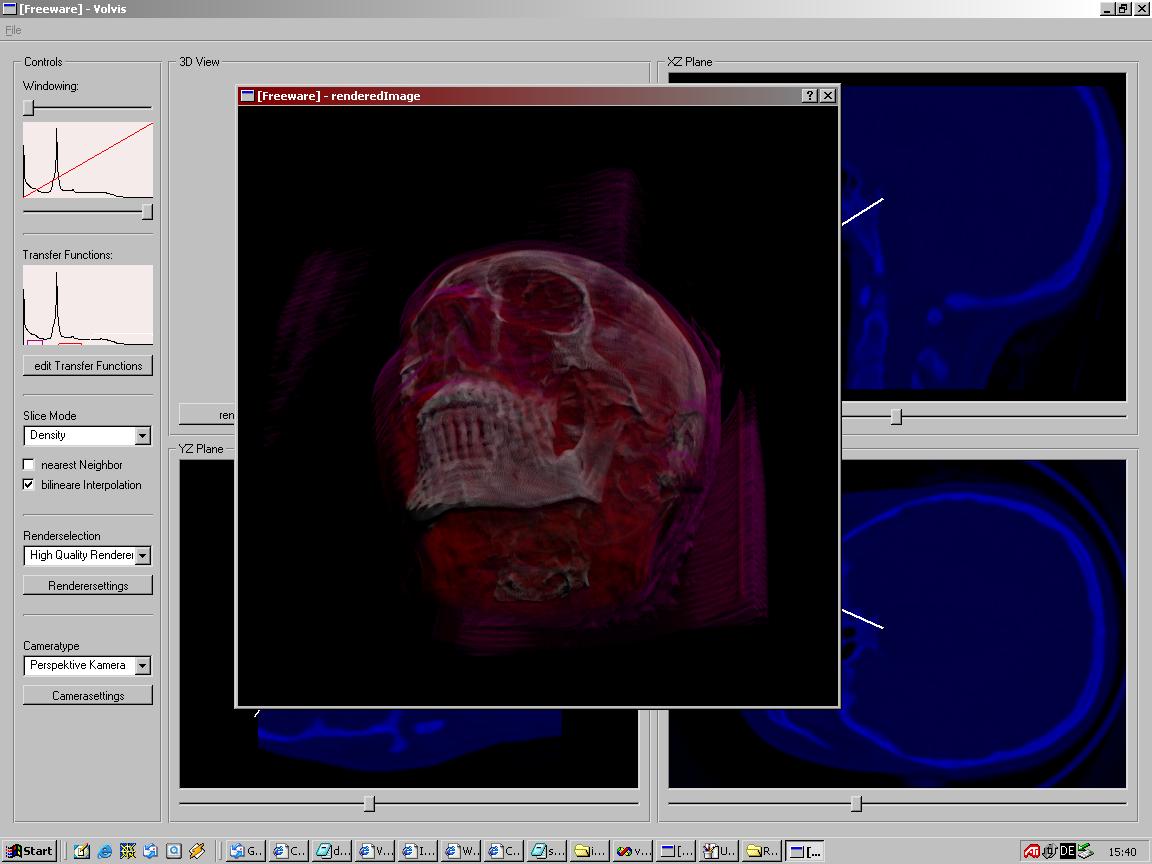