LU Visualisierung 2005
Statistische Analysen mit Parallelen Koordinaten

Parallele Koordinaten erlauben eine Darstellung von mehreren Dimensionen. Die Interaktionsmöglichkeiten dieser Visualisierung sollen genutzt werden, um statistische Analysen durchzuführen.
Zu diesem Zweck wurde ein k means Clustering, eine Hauptkomponentenanalyse (PCA) und die Berechnung der Mahalanobis und der robusten Distanz implementiert.
In einem zweiten Arbeitsschritt wurden zu den parallelen Koordinaten ein linked Scatterplot und eine Outlier Detection implementiert.

Beim k means Clustering-Algorithmus werden k zufällig gewählte Datenpunkte als Startclusterzentren gewählt. Anschließend werden die Datenpunkte jenem Cluster zugeordnet, der das näheste Clusterzentrum aufweist. Neue Clusterzentren werden berechnet, in dem die Datenpunkte eines Clusters gemittelt werden. Die Zuordnung der Datenpunkte und die Neuberechnung der Clusterzentren wird mehrmals wiederholt, bis sich die Clusterzentren nicht mehr oder nur geringfügig ändern, oder bis eine maximale Iterationszahl erreicht ist.
Für das Clustering können folgende Einstellungen vorgenommen werden:

• Anzahl der Cluster (k)
• Anzahl der maximalen Iterationen
• Minimale Updateschranke (Wenn kein Clusterzentrum ein Update erfährt, das diese Schranke übertrifft, wird der Clusterprozess gestoppt.)
• Auswahl und Gewichtung der Dimensionen nach denen geclustert werden soll.

Es können sowohl die Clusterzugehörigkeiten als auch die Distanzen der Datenpunkte zu ihrem Clusterzentrum abgespeichert werden. In dem folgenden Beispiel wurde ein Clustering für den Iris-Datensatz durchgeführt. Dieser Datensatz enthält vier verschiedene Messungen aufgrund deren man versucht, drei verschiedene Arten von Iris-Blumen zu unterscheiden. Das k means Clustering wurde nun auf diesen vier Messdimensionen durchgeführt. Drei Cluster wurden generiert

In der Graphik sind zunächst die vier Messdimensionen und als fünfte Dimension die Spezies zu sehen. Die Datenpunkte wurden gemäß der Clusterzugehörigkeit eingefärbt. Man kann daraus erkennen, dass der rote Cluster eine Spezies perfekt erkennt. Der blaue und der grüne Cluster teilen untereinander die beiden "ähnlichsten" Spezies auf.
Durch die Selektion von Datenpunkten mit hoher Distanz zu deren Clusterzentren kann man nun Datenpunkte identifizieren, die an den Rändern der Cluster liegen und somit wohl am ehesten der Clustereinteilung widersprechen bzw. auch anderen Clustern zugeordnet werden können.

In dieser Graphik sind zunächst wieder die vier Messdimensionen und als fünfte Dimension die Distanz der Datenpunkte zu deren Clusterzentren abgebildet. Durch die grüne Selektion werden Datenpunkte zu 100 % ausgewählt. Durch die darunterliegende blaue Selektion wird eine lineare Abschwächung der Auswahl von 100% auf 0% durchgeführt.

Die Mahalanobis Distanz gibt für jeden Datenpunkt an wie weit dieser vom Zentrum der Daten (unter Berücksichtigung der Streuung) entfernt ist. Sie wird wie folgt berechnet:

C(X) repräsentiert die Kovarianzmatrix und T(X) das komponentenweise arithmetische Mittel. Da sowohl das arithmetische Mittel als auch die Kovarianzmatrix durch Ausreißer stark beeinflusst werden kann, kann eine robuste Schätzung der Lokation (T(X)) und der Streuung (C(X)) verwendet werden um eine robuste Distanz zu ermitteln.

Um den Unterschied zwischen der Mahalanobis und der robusten Distanz aufzuzeigen wurde der künstliche Datensatz von Hawkins, Bradu, and Kass (1984) verwendet. Der Datensatz besteht aus 75 Beobachtungen, von denen die ersten 14 Ausreißer sind. Dies ist in folgender Abbildung zu erkennen.

Um diese Ausreißer zu automatisch zu detektieren wurde nun die Mahalanobis und die robuste Distanz berechnet und in den Parallelen Koordinaten angezeigt. Durch Selektieren der größten Werte der Mahalanobis Distanz werden auch "normale" Datenpunkte erfasst. Würde man nur die von der Menge der Datenpunkte hervorstehenden Werte selektieren, so würde man nicht alle Ausreißer erfassen. Im Gegensatz dazu separiert die robuste Distanz alle Ausreißer klar vom Hauptteil der Daten.

Die Hauptkomponentenanalyse berechnet die Eigenvektoren der Kovarianzmatrix und reiht sie nach deren Eigenwerten. Jener Eigenvektor mit dem größten Eigenwert stellt die erste Hauptkomponente dar. Auf diese ist der größte Anteil der Varianz der Daten abgebildet. So kann die Hauptkomponentenanalyse zur Dimensionsreduktion herangezogen werden. (Wie bei der Berechnung von der Distanz kann auch für die Hauptkomponentenanalyse eine robuste Schätzung für die Kovarianz verwendet werden.)
In folgendem Beispiel werden die vier Messdimensionen des Iris Datensatzes auf die erste Hauptkomponente abgebildet. Diese beschreibt (mit einer klassischen Schätzung für die Kovarianzmatrix) 92.5 % der Varianz in den Daten. In folgender Visualisierung sind die IDs der Datenpunkte, deren Projektion auf die erste Hauptkomponente und deren Spezies abgebildet. Sie sind gemäß ihrer Zugehörigkeit zu einer Spezies eingefärbt.

Aus dieser Graphik kann man erkennen, dass die vier Messdimensionen die blau eingefärbte Spezies sehr gut von den anderen separiert, während die beiden verbleibenden Spezies eine überschneidung in den Werten aufweist und ein Ausreißer aus der roten Spezies weit im Bereich der grünen liegt.

Der Großteil der Funktionalität des Programms kann über das Menü angesteuert werden. Über das Menü "File" können Daten in Form von CSV-Dateien geladen, Bilder der aktuellen Visualisierung exportiert und selektierte Daten ins CSV-Format exportiert werden.

Im Menü "Applications" können der linked 2D Scatterplot und die Outlier Detection aufgerufen werden. Im Menü "View" können die Fenster für das Steuern der Farbgebung und der Achsenansicht geöffnet werden. Über das Menü "Tools" können die Fenster für die statistischen Funktionen (Clustering, PCA, Distanzen) aufgerufen werden.

Farbgebung

Im Panel "Color types" kann ausgewählt werden, ob die Datenpunkte gemäß einer Selektion oder gemäß der Werte einer Dimension eingefärbt werden sollen.
Wird gemäß einer Selektion gefärbt, so kann man Farben für selektierte und nicht selektierte Datenpunkte festlegen, in dem man mit der rechten Maustaste auf die dafür vorgesehenen Farbrechtecke klickt. Für Datenpunkte, die Selektionswerte zwischen 0 und 1 haben, kann ein Farbverlauf definiert werden. "Linear transition" legt dabei einen Farbverlauf zwischen der Farbe für selektierte Datenpunkte und jene für nicht selektierte Datenpunkte fest. Bei "Advanced transition" können an jeder Stelle mittels Doppelklick Farbpunkte eingefügt werden. Mit erneutem Doppelklick können diese wieder gelöscht werden und mit einem rechten Mausklick kann die Farbe verändert werden. Diese Farbpunkte können auch verschoben werden.

Wird gemäß der Werte einer Dimension gefärbt, so kann zunächst festgelegt werden, nach welcher Dimension gefärbt werden soll. Ansonsten sind alle Einstellungen analog zur Färbung nach Selektion vorzunehmen. Anstatt der Farbe von selektierten und nicht selektierten Datenpunkten kann nun die Farbe für Datenpunkte mit maximalen und minimalen Wert in der spezifizierten Dimension festgelegt werden. Der Farbverlauf für die Werte dazwischen wird wieder analog festgelegt.

Achsenansicht

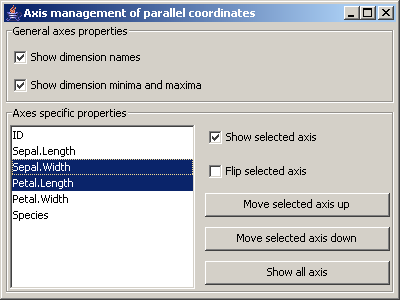
Zunächst können allgemeine Achseneinstellungen festgelegt werden (Anzeige von Dimensionsnamen und deren minimalen bzw. maximalen Wert).
Im Panel "Axes specific properties" können die gewünschten Achsen selektiert für diese festgelegt werden, ob sie sichtbar oder geflippt sein sollen. Weiters können die selektierten Achsen mit dem Button "Move selected axis up" in der Ansicht vorgereiht und mit "Move selected axis down" in der Ansicht nach hinten verschoben werden. Der Button "Show all axes" setzt alle Achsen auf sichtbar.

Clustering

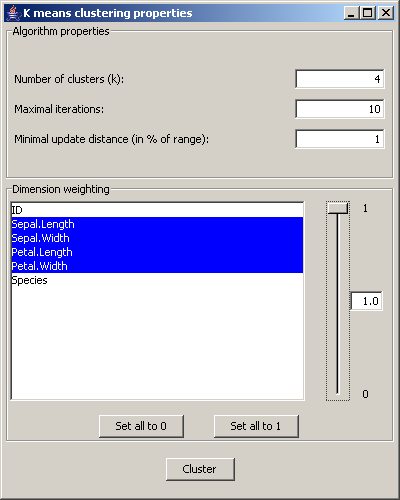
Im Panel "Algorithm properties" kann eingestellt werden wie viele Cluster erzeugt werden sollen, wie viele Iterationen der Algorithmus maximal laufen soll und ab welcher Update Schranke der Clusterzentren der Algorithmus terminieren soll. (Letzteres Maß wird in Prozent vom Range der Daten angegeben.)
Beim "Dimension weighting" werden jene Dimensionen ausgewählt, nach denen geclustert werden soll. Dabei können den Dimensionen verschiedene Gewichte zwischen 0 und 1 zugewiesen werden, um deren Einfluss auf das Clustering festzulegen.
Der Button "Cluster" startet den Clusteralgorithmus und fügt die Clustering Ergebnisse zum Datensatz hinzu.

Principal component analysis (PCA)

Im Panel "Type of pca" wird festgelegt ob die PCA auf der klassischen oder einer robusten Schätzung der Kovarianzmatrix beruht. Wurde die robuste Variante ausgewählt, so kann der User festlegen auf wieviel Prozent der Daten sich die robuste Schätzung beziehen soll.
Im Panel "PCA parameters" werden die Dimensionen ausgewählt, für welche die PCA durchgeführt werden soll. Mit einem Auswahlfeld kann festgelegt werden, wieviele Hauptkomponenten abgespeichert werden sollen. Für die gewählte Anzahl der Hauptkomponenten wird die beschriebene Varianz in Prozent angegeben. Schließlich kann noch der Name für die neuen Koordinatendimensionen der Datenpunkte, die abgespeichert werden, festgelegt werden.
Der Button "Add principal components to data" fügt die Koordinatendimensionen zum Datensatz hinzu.

Distances

Dieses Fenster wird analog zu jenem der PCA bedient.

Outlier Detection

Zunächst wird ein Fenster zum berechnen der robusten Distanz geöffnet. Dieses entspricht jenem der Distances, wobei allerdings keine Auswahl zwischen robuster und Mahalanobis Distanz vorgenommen werden kann. Anstatt die Distanz nun in den Daten abzuspeichern, wird sie in einem speziellen Scatterplot angezeigt.

Auf der X Achse ist die ID der Einträge im Datensatz aufgetragen. Auf der Y Achse ist die berechnete robuste Distanz geplottet. Eine Markierung zeigt die Entscheidungsgrenze, die Ausreißer von "normalen" Datenpunkten trennt an. Durch den Schieberegler auf der linken Seite kann eingestellt werden, wie viele "normale" Datenpunkte in Prozent im Datensatz erwartet werden. Demnach verändert sich die Grenze die das entsprechende Quantil der Chi-Quadrat Verteilung mit einem Freiheitsgrad von p entspricht. p repräsentiert die Anzahl der Dimensionen, die für die Berechnung der robusten Distanz herangezogen wurde.
Durch ein Menü kann man interaktiv auf den Ausreißern oder alternativ auf den "normalen" Daten weiterarbeiten.