
staircase-aware smoothing of medical surface meshes
This is an implementation staircase-aware mesh smoothing as proposed in the paper "Staircase-Aware Smoothing of Medical Surface Meshes" by Tobias Mönch, Simon Adler, and Bernhard Preim.
Generally, artifacts caused by noise and the discrete scan resolution can be reduced at several stages of the mesh generation process by using interpolation or smoothing methods. There exist numerous approaches to perform smoothing on the output mesh itself using a smoothing filter such as the Laplacian filter. Unfortunately, applying the filter uniformly to each vertex of the mesh also reduces small and possibly crucial features of the original data set and leads to volume shrinkage. As precision and resemblance to the real anatomy are vital for tasks such as preoperative surgical planning, it is important to create a mesh that is both accurate in shape and size and preserves all preservable features while removing all distracting artifacts.
Therefore, Mönch et al. propose the use of non-uniform filtering by calculating per-vertex smoothing weights according to the vertices' proximity to an artifact edge based on their normal vectors and the direction of the image stack. Since the resolution of the volume data gathered in the image acquisition process is usually considerably smaller in the image stack direction than inside the slices itself, staircase and plateau artifacts will occur in the triangulation process (Marching Cubes) whenever the object shape changes between two consecutive slices such that no continuous transition can be reconstructed. Thus, the side faces of the staircase artifacts will be parallel to the image stack direction while the faces on top of it will be orthogonal to it. In other words, for perfectly vertical faces, the dot product of the face's normal vector and the image stack direction will be 0, for horizontal faces it will be 1.
Using this face orientation relative to the image stack direction, Mönch et al. calculate an orientation change per vertex, which can be used to classify vertices at the edge of artifacts, because they will have incident faces with both parallel and orthogonal orientation. With this identification of edge vertices, all vertices can be weighted according to their proximity to an edge vertex in order to smooth not only the edge itself, but also the neighborhood. The result is a weight that can be multiplied with the weighting factor of every common smoothing filter, making it very useful for practice. According to this weight, non-uniform smoothing can be performed on the mesh such that vertices in the surrounding of artifacts will be strongly smoothed, while all features of non-artifact regions are preserved.
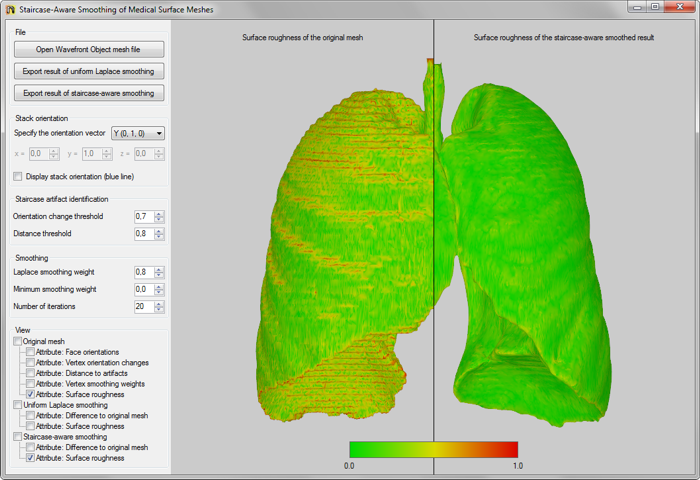
To demonstrate this technique, the proposed algorithm has been implemented in a .NET Framework 4.0 application using OpenGL via OpenTK for the rendering of the results. Wavefront Object (*.obj) mesh files can be imported and both uniform Laplacian smoothing and non-uniform staircase-aware smoothing can be applied to the mesh. The smoothed results can then be exported.
For easy comparison of the results of both smoothing methods as well as to visualize intermediate results of the implemented algorithm, several views can be juxtaposed. As an example, the screenshot above shows the surface roughness (calculated from a mean curvature estimation) for the original mesh (left) and the result of staircase-aware smoothing (right).
views
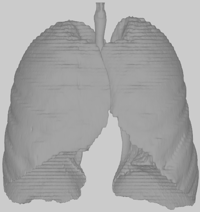
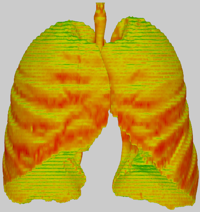

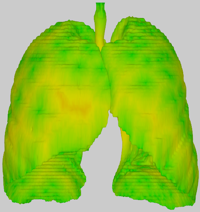
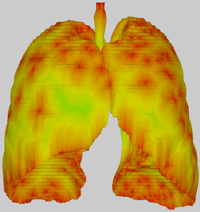
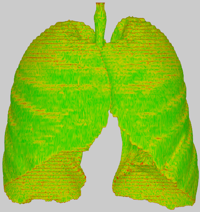
Original mesh - The unprocessed, diffuse shaded input mesh. The model used for this example, lungs.obj, is included in the download below.
Attribute: Face orientations - Per-face orientations relative to the stack orientation calculated as 1 - dot(face orientation, stack orientation).
Attribute: Vertex orientation changes - Per-vertex orientation changes based on the highest orientation change of adjacent faces relative to the stack orientation.
Attribute: Distance to artifacts - Per-vertex topological distance to the closest artifact vertex in the mesh. An artifact vertex is defined as a vertex which has an orientation change greater than a predefined threshold.
Attribute: Vertex smoothing weights - Per-vertex staircase-aware smoothing weights based on the minimum distance of each vertex to an artifact vertex.
Attribute: Surface roughness - Per-vertex roughness estimation of the mesh calculated as 1 - mean curvature.

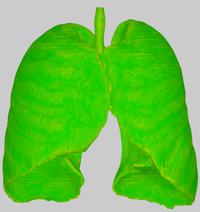
Uniform Laplace Smoothing - Diffuse shaded result of uniform Laplacian smoothing. Additionally, the approximate volume shrinkage relative to the original mesh is displayed.
Attribute: Difference to original mesh - Per-vertex normalized local distance to the original mesh to visualize the difference between the meshes.
Attribute: Surface roughness - Per-vertex roughness estimation of the mesh calculated as 1 - mean curvature.
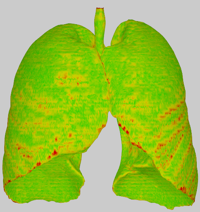
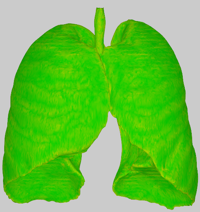
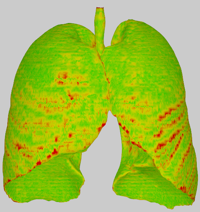
Staircase-aware Smoothing - Diffuse shaded result of staircase-aware smoothing. Additionally, the approximate volume shrinkage relative to the original mesh is displayed.
Attribute: Difference to original mesh - Per-vertex normalized local distance to the original mesh to visualize the difference between the meshes.
Attribute: Surface roughness - Per-vertex roughness estimation of the mesh calculated as 1 - mean curvature.
parameters
Stack orientation - The stack orientation is the most important parameter for the staircase artifact detection. The alignment of slices in the image stack prior to the triangulation and mesh creation specifies the orientation of plateau and staircase artifacts, so a wrong definition of this orientation leads to undesired results. It is specified as a three-dimensional vector which is normalized in the application before usage.
For a better understanding of the relation between the stack orientation and the face orientations, the stack orientation can be displayed.
Staircase artifact detection - In the paper by Mönch et al., two parameters are introduced to control the quality of the artifact detection.
To consider only vertices as artifact vertices which have a high orientation change, the orientation change threshold is used. The orientation change is a value between 0 and 1, where 0 indicates that all adjacent faces of a vertex have the exact same orientation and 1 indicates that at the vertex, the surface orientation changes by 90 degrees. Therefore, a higher threshold selects only hard edges, whereas a smaller threshold also includes smoother edges.
After the artifact vertices are detected, the minimum distance of each vertex to an artifact vertex and a smoothing weight based on this distance are calculated. In order to avoid smoothing of vertices very far away from any artifact region, the distance threshold is used to limit the distance to a specific range between 0 and 1. The distances are scaled such that 1 is the highest topological distance of any vertex of the mesh to an artifact, whereas an artifact vertex itself has a distance of 0. Therefore, a lower threshold restricts smoothing to regions close to artifacts.
Smoothing - Laplacian smoothing moves each vertex a bit into the direction of the centroid of all adjacent vertices. Therefore, a Laplace smoothing weight has to be specified to control the strength of this vertex displacement. For a smooth mesh, the process is iterated a few times, thus the number of iterations is required, too.
When using non-uniform smoothing based on per-vertex smoothing weights, it might be desirable to define a minimum smoothing weight such that the whole mesh is uniformly smoothed and additional smoothing is performed at the artifact regions.
download
Download the source code, binaries for Windows, and sample data sets (19.2 MB).
The data sets have been retrieved from http://pubimage.hcuge.ch:8080/.
Please note that the application requires the .NET Framework 4.0 Client Profile to function properly.