Speaker: Diana Marin
Abstract:
Extrapolating information from incomplete data is a key human skill, enabling us to infer patterns and make predictions from limited observations. A prime example is our ability to perceive coherent shapes from seemingly random point sets, a key aspect of cognition. However, data reconstruction becomes challenging when no predefined rules exist, as it is unclear how to connect the data or infer patterns. In computer graphics, a major goal is to replicate this human ability by developing algorithms that can accurately reconstruct original structures or extract meaningful information from raw, disconnected data.
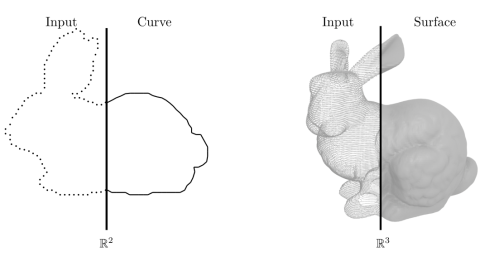
The contributions of this thesis deal with point cloud reconstruction, leveraging proximity-based methods, with a particular focus on a specific proximity-encoding data structure - the spheres-of-influence graph (SIG). We discuss curve reconstruction, where we automate the game of connecting the dots to create contours, providing theoretical guarantees for our method. We obtain the best results compared to similar methods for manifold curves. We extend our curve reconstruction to manifolds, overcoming the challenges of moving to different domains, and extending our theoretical guarantees. We are able to reconstruct curves from sparser inputs compared to the state-of-the-art, and we explore various settings in which these curves can live. We investigate the properties of the SIG as a parameter-free proximity encoding structure of three-dimensional point clouds. We introduce new spatial bounds for the SIG neighbors as a theoretical contribution. We analyze how close the encoding is to the ground truth surface compared to the commonly used kNN graphs, and we evaluate our performance in the context of normal estimation as an application. Lastly, we introduce SING, a stability-incorporated neighborhood graph, a useful tool with various applications, such as clustering, and with a strong theoretical background in topological data analysis.