Feature-Preserving Volume Filtering

Information

• Publication Type: Conference Paper
• Workgroup(s)/Project(s):
  • ADAPT: Advanced Diagnosis, Analysis and Planning Tools (in Medicine)
• Date: May 2002
• Publisher: ACM
• Booktitle: Data Visualization 2002
• Pages: 105 – 114
• Keywords: antialiasing, noise filtering, derivative and gradient estimation, feature-preserving smoothing, direct volume rendering

Abstract

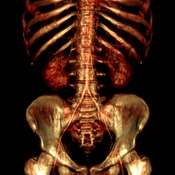
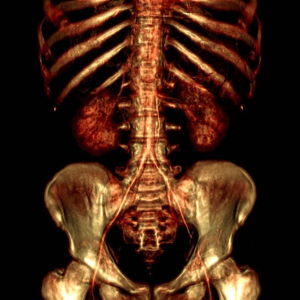
In this paper a feature-preserving volume filtering method is presented. The basic idea is to minimize a three-component global error function penalizing the density and gradient errors and the curvature of the unknown filtered function. The optimization problem leads to a large linear equation system defined by a sparse coefficient matrix. We will show that such an equation system can be efficiently solved in frequency domain using fast Fourier transformation (FFT). For the sake of clarity, first we illustrate our method on a 2D example which is a dedithering problem. Afterwards the 3D extension is discussed in detail since we propose our method mainly for volume filtering. We will show that the 3D version can be efficiently used for elimination of the typical staircase artifacts of direct volume rendering without losing fine details. Unlike local filtering techniques, our novel approach ensures a global smoothing effect. Previous global 3D methods are restricted to binary volumes or segmented iso-surfaces and they are based on area minimization of one single reconstructed surface. In contrast, our method is a general volume-filtering technique, implicitly smoothing all the iso-surfaces at the same time. Although the strength of the presented algorithm is demonstrated on a specific 2D and a specific 3D application, it is considered as a general mathematical tool for processing images and volumes.

Additional Files and Images

Weblinks

No further information available.

BibTeX

@inproceedings{Neumann-2002-Fea,
  title =      "Feature-Preserving Volume Filtering",
  author =     "L\'{a}szl\'{o} Neumann and Bal\'{a}zs Cs\'{e}bfalvi and Ivan
               Viola and Matej Mlejnek and Eduard Gr\"{o}ller",
  year =       "2002",
  abstract =   "In this paper a feature-preserving volume filtering method
               is presented. The basic idea is to minimize a
               three-component global error function penalizing the density
               and gradient errors and the curvature of the unknown
               filtered function. The optimization problem leads to a large
               linear equation system defined by a sparse coefficient
               matrix. We will show that such an equation system can be
               efficiently solved in frequency domain using fast Fourier
               transformation (FFT). For the sake of clarity, first we
               illustrate our method on a 2D example which is a dedithering
               problem. Afterwards the 3D extension is discussed in detail
               since we propose our method mainly for volume filtering. We
               will show that the 3D version can be efficiently used for
               elimination of the typical staircase artifacts of direct
               volume rendering without losing fine details. Unlike local
               filtering techniques, our novel approach ensures a global
               smoothing effect. Previous global 3D methods are restricted
               to binary volumes or segmented iso-surfaces and they are
               based on area minimization of one single reconstructed
               surface. In contrast, our method is a general
               volume-filtering technique, implicitly smoothing all the
               iso-surfaces at the same time. Although the strength of the
               presented algorithm is demonstrated on a specific 2D and a
               specific 3D application, it is considered as a general
               mathematical tool for processing images and volumes.",
  month =      may,
  publisher =  "ACM",
  booktitle =  "Data Visualization 2002",
  pages =      "105--114",
  keywords =   "antialiasing, noise filtering, derivative and gradient
               estimation, feature-preserving smoothing, direct volume
               rendering",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2002/Neumann-2002-Fea/",
}