Gaussian-Product Subdivision Surfaces

Information

• Publication Type: Journal Paper with Conference Talk
• Workgroup(s)/Project(s):
  • Rendering and Modeling
• Date: July 2019
• Journal: ACM Transactions on Graphics
• Volume: 38
• Open Access: yes
• Number: 4
• Location: Los Angeles, USA
• Lecturer: Reinhold Preiner
• ISSN: 0730-0301
• Event: ACM SIGGRAPH 2019
• DOI: 10.1145/3306346.3323026
• Conference date: 28. July 2019 – 1. August 2019
• Pages: 35:1 – 35:11
• Keywords: Gaussian mixtures, surface reconstruction, subdivision surfaces

Abstract

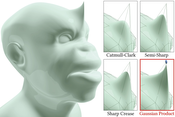
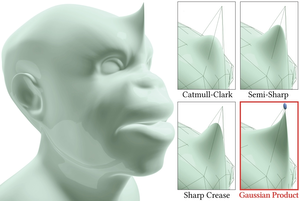
Probabilistic distribution models like Gaussian mixtures have shown great potential for improving both the quality and speed of several geometric operators. This is largely due to their ability to model large fuzzy data using only a reduced set of atomic distributions, allowing for large compression rates at minimal information loss. We introduce a new surface model that utilizes these qualities of Gaussian mixtures for the definition and control of a parametric smooth surface. Our approach is based on an enriched mesh data structure, which describes the probability distribution of spatial surface locations around each vertex via a Gaussian covariance matrix. By incorporating this additional covariance information, we show how to define a smooth surface via a nonlinear probabilistic subdivision operator based on products of Gaussians, which is able to capture rich details at fixed control mesh resolution. This entails new applications in surface reconstruction, modeling, and geometric compression.

Additional Files and Images

Weblinks

• Entry in the publication database of TU-Wien
• DOI: 10.1145/3306346.3323026

BibTeX

@article{Preiner_2019,
  title =      "Gaussian-Product Subdivision Surfaces",
  author =     "Reinhold Preiner and Tamy Boubekeur and Michael Wimmer",
  year =       "2019",
  abstract =   "Probabilistic distribution models like Gaussian mixtures
               have shown great potential for improving both the quality
               and speed of several geometric operators. This is largely
               due to their ability to model large fuzzy data using only a
               reduced set of atomic distributions, allowing for large
               compression rates at minimal information loss. We introduce
               a new surface model that utilizes these qualities of
               Gaussian mixtures for the definition and control of a
               parametric smooth surface. Our approach is based on an
               enriched mesh data structure, which describes the
               probability distribution of spatial surface locations around
               each vertex via a Gaussian covariance matrix. By
               incorporating this additional covariance information, we
               show how to define a smooth surface via a nonlinear
               probabilistic subdivision operator based on products of
               Gaussians, which is able to capture rich details at fixed
               control mesh resolution. This entails new applications in
               surface reconstruction, modeling, and geometric compression.",
  month =      jul,
  journal =    "ACM Transactions on Graphics",
  volume =     "38",
  number =     "4",
  issn =       "0730-0301",
  doi =        "10.1145/3306346.3323026",
  pages =      "35:1--35:11",
  keywords =   "Gaussian mixtures, surface reconstruction, subdivision
               surfaces",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2019/Preiner_2019/",
}