ManyLands: A Journey Across 4D Phase Space of Trajectories

Information

• Publication Type: Journal Paper with Conference Talk
• Workgroup(s)/Project(s): not specified
• Date: October 2019
• Journal: Computer Graphics Forum
• Volume: 38
• Number: 7
• Location: Seoul, South Korea
• Lecturer: Aleksandr Amirkhanov
• Event: Pacific Graphics 2019
• DOI: 10.1111/cgf.13828
• Call for Papers: Call for Paper
• Conference date: 1. January 2019 – 7. June 2019
• Pages: 191 – 202
• Keywords: Visual analytics, Web-based interaction

Abstract

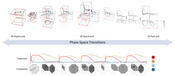
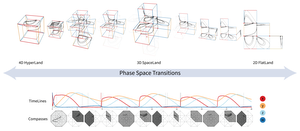
Mathematical models of ordinary differential equations are used to describe and understand biological phenomena. These models are dynamical systems that often describe the time evolution of more than three variables, i.e., their dynamics take place in a multi-dimensional space, called the phase space. Currently, mathematical domain scientists use plots of typical trajectories in the phase space to analyze the qualitative behavior of dynamical systems. These plots are called phase portraits and they perform well for 2D and 3D dynamical systems. However, for 4D, the visual exploration of trajectories becomes challenging, as simple subspace juxtaposition is not sufficient. We propose ManyLands to support mathematical domain scientists in analyzing 4D models of biological systems. By describing the subspaces as Lands, we accompany domain scientists along a continuous journey through 4D HyperLand, 3D SpaceLand, and 2D FlatLand, using seamless transitions. The Lands are also linked to 1D TimeLines. We offer an additional dissected view of trajectories that relies on small-multiple compass-alike pictograms for easy navigation across subspaces and trajectory segments of interest. We show three use cases of 4D dynamical systems from cell biology and biochemistry. An informal evaluation with mathematical experts confirmed that ManyLands helps them to visualize and analyze complex 4D dynamics, while facilitating mathematical experiments and simulations.

Additional Files and Images

Weblinks

• ManyLands repository
• E-print
• DOI: 10.1111/cgf.13828

BibTeX

@article{amirkhanov-2019-manylands,
  title =      "ManyLands: A Journey Across 4D Phase Space of Trajectories",
  author =     "Aleksandr Amirkhanov and Ilona Kosiuk and Peter Szmolyan and
               Artem Amirkhanov and Gabriel Mistelbauer and Eduard
               Gr\"{o}ller and Renata Raidou",
  year =       "2019",
  abstract =   "Mathematical models of ordinary differential equations are
               used to describe and understand biological phenomena. These
               models are dynamical systems that often describe the time
               evolution of more than three variables, i.e., their dynamics
               take place in a multi-dimensional space, called the phase
               space. Currently, mathematical domain scientists use plots
               of typical trajectories in the phase space to analyze the
               qualitative behavior of dynamical systems. These plots are
               called phase portraits and they perform well for 2D and 3D
               dynamical systems. However, for 4D, the visual exploration
               of trajectories becomes challenging, as simple subspace
               juxtaposition is not sufficient. We propose ManyLands to
               support mathematical domain scientists in analyzing 4D
               models of biological systems. By describing the subspaces as
               Lands, we accompany domain scientists along a continuous
               journey through 4D HyperLand, 3D SpaceLand, and 2D FlatLand,
               using seamless transitions. The Lands are also linked to 1D
               TimeLines. We offer an additional dissected view of
               trajectories that relies on small-multiple compass-alike
               pictograms for easy navigation across subspaces and
               trajectory segments of interest. We show three use cases of
               4D dynamical systems from cell biology and biochemistry. An
               informal evaluation with mathematical experts confirmed that
               ManyLands helps them to visualize and analyze complex 4D
               dynamics, while facilitating mathematical experiments and
               simulations.",
  month =      oct,
  journal =    "Computer Graphics Forum",
  volume =     "38",
  number =     "7",
  doi =        "10.1111/cgf.13828",
  pages =      "191--202",
  keywords =   "Visual analytics, Web-based interaction",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2019/amirkhanov-2019-manylands/",
}