Stefan Ohrhallinger, Michael WimmerORCID iD
FitConnect: Connecting Noisy 2D Samples by Fitted Neighborhoods
Computer Graphics Forum, 38(1):126-137, February 2019. [paper] [Replicability Source Code]

Information

Abstract

We propose a parameter-free method to recover manifold connectivity in unstructured 2D point clouds with high noise in terms of the local feature size. This enables us to capture the features which emerge out of the noise. To achieve this, we extend the reconstruction algorithm HNN-Crust, which connects samples to two (noise-free) neighbors and has been proven to output a manifold for a relaxed sampling condition. Applying this condition to noisy samples by projecting their k-nearest neighborhoods onto local circular fits leads to multiple candidate neighbor pairs and thus makes connecting them consistently an NP-hard problem. To solve this efficiently, we design an algorithm that searches that solution space iteratively on different scales of k. It achieves linear time complexity in terms of point count plus quadratic time in the size of noise clusters. Our algorithm FitConnect extends HNN-Crust seamlessly to connect both samples with and without noise, performs as local as the recovered features and can output multiple open or closed piece-wise curves. Incidentally, our method simplifies the output geometry by eliminating all but a representative point from noisy clusters. Since local neighborhood fits overlap consistently, the resulting connectivity represents an ordering of the samples along a manifold. This permits us to simply blend the local fits for denoising with the locally estimated noise extent. Aside from applications like reconstructing silhouettes of noisy sensed data, this lays important groundwork to improve surface reconstruction in 3D. Our open-source algorithm is available online.

Additional Files and Images

Additional images and videos

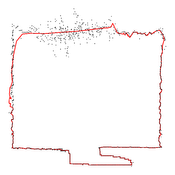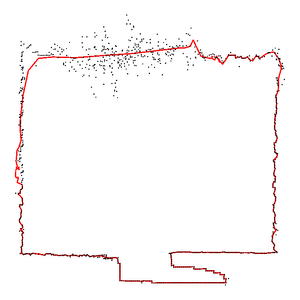
image: Manifold curve fitted samples with highly varying noise image: Manifold curve fitted samples with highly varying noise

Additional files

paper: preprint paper: preprint

Weblinks

BibTeX

@article{ohrhallinger_stefan-2018-cgf,
  title =      "FitConnect: Connecting Noisy 2D Samples by Fitted
               Neighborhoods",
  author =     "Stefan Ohrhallinger and Michael Wimmer",
  year =       "2019",
  abstract =   "We propose a parameter-free method to recover manifold
               connectivity in unstructured 2D point clouds with high noise
               in terms of the local feature size. This enables us to
               capture the features which emerge out of the noise. To
               achieve this, we extend the reconstruction algorithm
               HNN-Crust, which connects samples to two (noise-free)
               neighbors and has been proven to output a manifold for a
               relaxed sampling condition. Applying this condition to noisy
               samples by projecting their k-nearest neighborhoods onto
               local circular fits leads to multiple candidate neighbor
               pairs and thus makes connecting them consistently an NP-hard
               problem. To solve this efficiently, we design an algorithm
               that searches that solution space iteratively on different
               scales of k. It achieves linear time complexity in terms of
               point count plus quadratic time in the size of noise
               clusters. Our algorithm FitConnect extends HNN-Crust
               seamlessly to connect both samples with and without noise,
               performs as local as the recovered features and can output
               multiple open or closed piece-wise curves. Incidentally, our
               method simplifies the output geometry by eliminating all but
               a representative point from noisy clusters. Since local
               neighborhood fits overlap consistently, the resulting
               connectivity represents an ordering of the samples along a
               manifold. This permits us to simply blend the local fits for
               denoising with the locally estimated noise extent. Aside
               from applications like reconstructing silhouettes of noisy
               sensed data, this lays important groundwork to improve
               surface reconstruction in 3D. Our open-source algorithm is
               available online.",
  month =      feb,
  journal =    "Computer Graphics Forum",
  volume =     "38",
  number =     "1",
  issn =       "1467-8659",
  doi =        "10.1111/cgf.13395",
  pages =      "126--137",
  keywords =   "curve fitting, noisy samples, guarantees, curve
               reconstruction",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2019/ohrhallinger_stefan-2018-cgf/",
}