Feature-Sized Sampling for Vector Line Art

Information

• Publication Type: Conference Paper
• Workgroup(s)/Project(s):
  • Modeling the World at Scale
• Date: October 2023
• Open Access: yes
• Lecturer: Stefan Ohrhallinger
• Event: Pacific Graphics, Daejeon, South Korea, 2023
• DOI: https://doi.org/10.2312/pg.20231268
• Booktitle: Proceedings of the 31th Pacific Conference on Computer Graphics and Applications
• Pages: 1 – 2
• Keywords: sampling, vector line art, meshing

Abstract

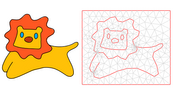
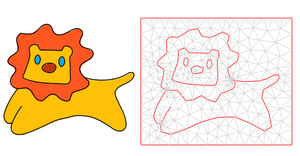
By introducing a first-of-its-kind quantifiable sampling algorithm based on feature size, we present a fresh perspective on the practical aspects of planar curve sampling. Following the footsteps of ε-sampling, which was originally proposed in the context of curve reconstruction to offer provable topological guarantees [ABE98] under quantifiable bounds, we propose an arbitrarily precise ε-sampling algorithm for sampling smooth planar curves (with a prior bound on the minimum feature size of the curve). This paper not only introduces the first such algorithm which provides user-control and quantifiable precision but also highlights the importance of such a sampling process under two key contexts: 1) To conduct a first study comparing theoretical sampling conditions with practical sampling requirements for reconstruction guarantees that can further be used for analysing the upper bounds of ε for various reconstruction algorithms with or without proofs, 2) As a feature-aware sampling of vector line art that can be used for applications such as coloring and meshing.

Additional Files and Images

Weblinks

• talk
• DOI: https://doi.org/10.2312/pg.20231268

BibTeX

@inproceedings{ohrhallinger_stefan-2023-con,
  title =      "Feature-Sized Sampling for Vector Line Art",
  author =     "Stefan Ohrhallinger and Amal Dev Parakkat and Pooran Memari",
  year =       "2023",
  abstract =   "By introducing a first-of-its-kind quantifiable sampling
               algorithm based on feature size, we present a fresh
               perspective on the practical aspects of planar curve
               sampling. Following the footsteps of ε-sampling, which was
               originally proposed in the context of curve reconstruction
               to offer provable topological guarantees [ABE98] under
               quantifiable bounds, we propose an arbitrarily precise
               ε-sampling algorithm for sampling smooth planar curves
               (with a prior bound on the minimum feature size of the
               curve). This paper not only introduces the first such
               algorithm which provides user-control and quantifiable
               precision but also highlights the importance of such a
               sampling process under two key contexts: 1) To conduct a
               first study comparing theoretical sampling conditions with
               practical sampling requirements for reconstruction
               guarantees that can further be used for analysing the upper
               bounds of ε for various reconstruction algorithms with or
               without proofs, 2) As a feature-aware sampling of vector
               line art that can be used for applications such as coloring
               and meshing. ",
  month =      oct,
  event =      "Pacific Graphics, Daejeon, South Korea, 2023",
  doi =        "https://doi.org/10.2312/pg.20231268",
  booktitle =  "Proceedings of the 31th Pacific Conference on Computer
               Graphics and Applications",
  pages =      "1--2",
  keywords =   "sampling, vector line art, meshing",
  URL =        "https://www.cg.tuwien.ac.at/research/publications/2023/ohrhallinger_stefan-2023-con/",
}