Information
- Publication Type: Journal Paper with Conference Talk
- Workgroup(s)/Project(s):
- Date: June 2024
- Journal: Computer Graphics Forum
- Volume: 43
- Number: 5
- Location: Boston
- Lecturer: Diana Marin
- Article Number: e15136
- ISSN: 1467-8659
- Event: Symposium on Geometry Processing
- DOI: 10.1111/cgf.15136
- Pages: 14
- Publisher: WILEY
- Conference date: 24. June 2024 – 26. June 2024
- Pages: - – -
- Keywords: CCS Concepts, Graph algorithms, Mesh geometry models, Paths and connectivity problems
Abstract
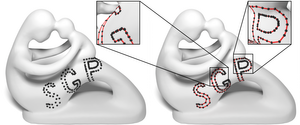
Reconstructing 2D curves from sample points has long been a critical challenge in computer graphics, finding essential applications in vector graphics. The design and editing of curves on surfaces has only recently begun to receive attention, primarily relying on human assistance, and where not, limited by very strict sampling conditions. In this work, we formally improve on the state-of-the-art requirements and introduce an innovative algorithm capable of reconstructing closed curves directly on surfaces from a given sparse set of sample points. We extend and adapt a state-of-the-art planar curve reconstruction method to the realm of surfaces while dealing with the challenges arising from working on non-Euclidean domains. We demonstrate the robustness of our method by reconstructing multiple curves on various surface meshes. We explore novel potential applications of our approach, allowing for automated reconstruction of curves on Riemannian manifolds.Additional Files and Images
Weblinks
- Entry in reposiTUm (TU Wien Publication Database)
- Entry of the presentation in reposiTUm (TU Wien Publication Database)
- DOI: 10.1111/cgf.15136
BibTeX
@article{marin-2024-rcf,
title = "Reconstructing Curves from Sparse Samples on Riemannian
Manifolds",
author = "Diana Marin and Filippo Maggioli and Simone Melzi and Stefan
Ohrhallinger and Michael Wimmer",
year = "2024",
abstract = "Reconstructing 2D curves from sample points has long been a
critical challenge in computer graphics, finding essential
applications in vector graphics. The design and editing of
curves on surfaces has only recently begun to receive
attention, primarily relying on human assistance, and where
not, limited by very strict sampling conditions. In this
work, we formally improve on the state-of-the-art
requirements and introduce an innovative algorithm capable
of reconstructing closed curves directly on surfaces from a
given sparse set of sample points. We extend and adapt a
state-of-the-art planar curve reconstruction method to the
realm of surfaces while dealing with the challenges arising
from working on non-Euclidean domains. We demonstrate the
robustness of our method by reconstructing multiple curves
on various surface meshes. We explore novel potential
applications of our approach, allowing for automated
reconstruction of curves on Riemannian manifolds.",
month = jun,
journal = "Computer Graphics Forum",
volume = "43",
number = "5",
articleno = "e15136",
issn = "1467-8659",
doi = "10.1111/cgf.15136",
pages = "14",
publisher = "WILEY",
pages = "----",
keywords = "CCS Concepts, Graph algorithms, Mesh geometry models, Paths
and connectivity problems",
URL = "https://www.cg.tuwien.ac.at/research/publications/2024/marin-2024-rcf/",
}