Betrachten wir zuerst ein einfaches Beispiel:

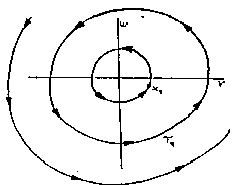
Ein Pendel ist ein periodisches System, dessen Verhalten sich durch die momentane Auslenkung w und die Momentangeschwindigkeit v charakterisieren läßt. Schwingt nun dieses Pendel und wird es durch nichts - auch nicht durch Reibung - beeinflußt, dann kann man das Verhalten wie oben gezeigt darstellen. Ein Punkt x1 = (w1;v1) in der Abbildung beschreibt einen Zustand des Systems. Wie sich dieser Zustand im Laufe der Zeit verändert, ist durch einzelne Trajektorien (Kurven mit Richtung z.B. t1) durch den Zustandsraum (hier 2D) skizziert.
Fügen wir dem System nun eine bremsende Kraft, nämlich die der Reibung, hinzu, dann verändert sich auch der Graph, der das Systemverhalten beschreibt.

Mit zunehmender Zeit wird das Pendel immer weniger ausschwingen und wird irgendwann zum Stillstand kommen. Folgt man der Spirale von außen nach innen, so sieht man, daß die Amplitude der Schwingung abnimmt; das heißt, daß sowohl die maximale Auslenkung als auch die maximale Geschwindigkeit abnehmen. Irgendwann wird das Pendel stehenbleiben. In der Abbildung ist der diesem Zustand entsprechende Punkt der Ursprung. Der Ursprung ist das Zentrum des spiralförmigen Graphen. Einen Punkt wie diesen, der alle Punkte seiner (näheren) Umgebung anzieht nennt man auch Attraktor. Darüber hinaus ist dieser Punkt ein Fixpunkt, das heißt, daß dieser Zustand des Systems - einmal erreicht - nie wieder verlassen werden kann. (Ein stehendes Pendel wird ohne Krafteinwirkung ja sicherlich nicht irgendwann plötzlich zu schwingen beginnen.)
