Die Hopf-Bifurkation
Die Hopf-Bifurkation
Die Hopf-Bifurkation kann in verschiedenen
Konstellationen auftreten:
man spricht auch von der Hopf-Bifurkation und von der verallgemeinerten
(entarteten) Hopf-Bifurkation. Beiden gemeinsam ist, daß sie eine
Hopf-Singularität besitzen. Es wird davon ausgegangen, daß diese
im Ursprung sitzt. Im weiteren wird nur auf die normale Hopfbifurkation
eingegangen.
Hopf-Singularitäten
Wenn wir eine Singularität durch die
Entartungsbedingung Tr J(F(
 )) = 0 und die Nicht-Entartungsbedingungen
det J(F(
)) = 0 und die Nicht-Entartungsbedingungen
det J(F( )) > 0 und
a1
)) > 0 und
a1 0
charakterisieren können, so wird diese nicht-entartete
Hopf-Singularität genannt, während eine Singularität
mit gleichen Voraussetzungen, aber mit den ersten k Elementen
ak gleich Null entartete Hopf-Singularität
genannt wird. Die Anzahl der ak = 0 bestimmt den
Entartungsgrad der Singularität. Mit
a1
0
charakterisieren können, so wird diese nicht-entartete
Hopf-Singularität genannt, während eine Singularität
mit gleichen Voraussetzungen, aber mit den ersten k Elementen
ak gleich Null entartete Hopf-Singularität
genannt wird. Die Anzahl der ak = 0 bestimmt den
Entartungsgrad der Singularität. Mit
a1 0
erhalten wir also die am geringsten entartete Hopf-Singularität
(man beachte, daß diese
3-Jet
determiniert ist).
0
erhalten wir also die am geringsten entartete Hopf-Singularität
(man beachte, daß diese
3-Jet
determiniert ist).
Was soll das alles? Ein Beispiel bitte!
-
Um den Sachverhalt zu veranschaulichen, betrachten wir ein System mit einer
Hopf-Bifurkation im Ursprung:
 1 = x2 + x1µ
(1 - x12 - x22)
1 = x2 + x1µ
(1 - x12 - x22)
 2 = -x1 + x2µ
(1 - x12 - x22)
2 = -x1 + x2µ
(1 - x12 - x22)
-
Betrachten wir nun, welche Entartungsbedingungen und Nicht-
Entartungsbedingungen erfüllt sind. Zunächst berechnen wir uns
die Jakobimatrix des Systems. Diese ist gegeben durch
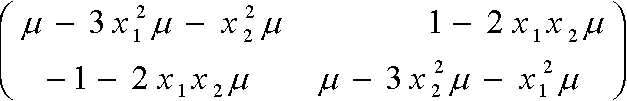
-
Wenn wir für x und y null einsetzen, so berechnet sich die
Determinante von (2) durch
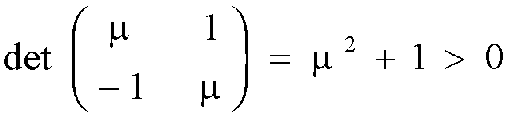
-
Die erste Nicht-Entartungsbedingung ist also erfüllt, die
Entartungsbedingung, welche verlangt, daß die Spur der Matrix
gleich null ist, fordert daher folgendes:
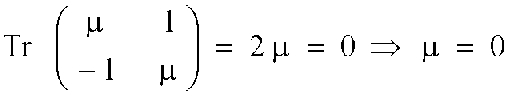
Das bedeudet aber, daß für µ = 0 auf jeden Fall eine Hopf-
Bifurkation stattfindet. Den genauen Entartungsgrad über die
Normalform zu bestimmen ist mit längeren Berechnungen verbunden und
wird hier nicht näher ausgeführt.
-
Trotzdem wollen wir versuchen, eine anschauliche Herleitung für das
Aussehen einer Hopf-Bifurkation zu liefern. Zunächst wollen wir das
System linearisieren durch
 '
1 = µx'1 + x'2
'
1 = µx'1 + x'2
 '
2 = -x'1 + µx'2
'
2 = -x'1 + µx'2
wobei x'1 und x'2 kleine Störungen
um den Fixpunkt sind (wir nehmen also x1 =
 1 +
x'1 und x2 =
1 +
x'1 und x2 =
 2 + x'2 an).
2 + x'2 an).
-
Es gilt nun also in Matrixschreibweise
 ' = Ax',
' = Ax',

Die Eigenwerte werden durch det(A - lambda*I) = 0 ermittelt und
ergeben sich als lambda1 = µ + i und
lambda2 = µ - i. Daher muß das Equilibrium
für µ < 0 lokal stabil und für µ > 0 lokal instabil sein. Man
stellt fest, daß für µ = 0 keine Stabilitätsaussage
getroffen werden kann. Um festzustellen, was wirklich passiert, wenn das
System seinen Stabilitätszustand ändert, wollen wir das
Differentialgleichungssystem in Polarkoordinaten umwandeln.
-
Es gilt nun also in Polarkoordinaten-Schreibweise
 = µr(1 - r2)
= µr(1 - r2)
 = -1"
= -1"
Die erste Gleichung von (7) kann man analytisch
lösen. Die Zwischenschritte werden hier überspringen und
gleich das Ergebnis präsentiert (der interessierte Leser findet
alle nötigen Umformungen in
[Tson92]).
-
Daraus folgt
r2(t) = r02
/[r02 + (1 - r02)
e-2µt]
Man sieht daraus sofort, daß für µ < 0 r(t) mit der Zeit
gegen 0 geht. Da die Winkeländerung konstant ist (7)
, muß also der Nullpunkt spiralartig anziehend sein. Weiters
sieht man, daß r(t) für t gegen Unendlich gegen
1 strebt, wenn µ > 0 gilt. Das System hat also einen anziehenden Zyklus mit
einem Radius 1.
Darstellung von Hopf-Bifurkationen
Die Hopf-Bifurkation läßt sich in zwei
Arten unterteilen, die
Supercritical Hopf-Bifurkation
und die
Subcritical Hopf-Bifurkation.
[<= Subcritical Hopf-Bifurkation]
[== Hopf-Bifurkation]
[=> Supercritical Hopf-Bifurkation]
 )) = 0 und die Nicht-Entartungsbedingungen
det J(F(
)) = 0 und die Nicht-Entartungsbedingungen
det J(F( )) > 0 und
a1
)) > 0 und
a1 0
charakterisieren können, so wird diese nicht-entartete
Hopf-Singularität genannt, während eine Singularität
mit gleichen Voraussetzungen, aber mit den ersten k Elementen
ak gleich Null entartete Hopf-Singularität
genannt wird. Die Anzahl der ak = 0 bestimmt den
Entartungsgrad der Singularität. Mit
a1
0
charakterisieren können, so wird diese nicht-entartete
Hopf-Singularität genannt, während eine Singularität
mit gleichen Voraussetzungen, aber mit den ersten k Elementen
ak gleich Null entartete Hopf-Singularität
genannt wird. Die Anzahl der ak = 0 bestimmt den
Entartungsgrad der Singularität. Mit
a1 0
erhalten wir also die am geringsten entartete Hopf-Singularität
(man beachte, daß diese
3-Jet
determiniert ist).
0
erhalten wir also die am geringsten entartete Hopf-Singularität
(man beachte, daß diese
3-Jet
determiniert ist).
 1 = x2 + x1µ
(1 - x12 - x22)
1 = x2 + x1µ
(1 - x12 - x22)
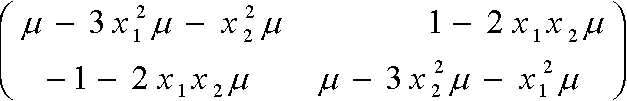
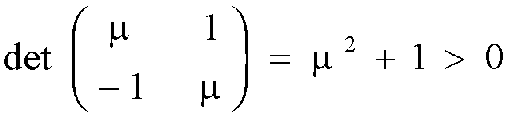
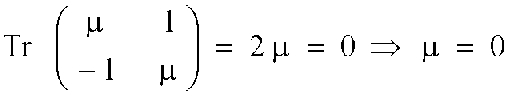

 = µr(1 - r2)
= µr(1 - r2)
 = -1"
= -1"