Einleitung
Das erste Beispiel beschäftigt sich mit der Vorverarbeitung volumetrischer Daten. Für die spätere Visualisierung der Daten ist es notwendig, zusätzliche Informationen aus den ursprünglichen Daten abzuleiten. Außerdem wird im ersten Beispiel das Visualization Mapping behandelt, d.h. die Abbildung der vorliegenden Daten auf visuell leicht erfassbare Größen.
Beschreibung
In diesem Beispiel soll im ersten Schritt der Gradient aus den Daten extrahiert werden. Der Gradient beschreibt die Richtung der größten Änderung in den Datenwerten an einer bestimmten Stelle des Volumens. In der Visualisierung wird der Gradient benötigt um später die Visualisierung zu verbessern.
Die Berechnung der Gradienten kann im Allgemeinen auch als ein Filterprozess mittels Faltung gesehen werden. Es wird dabei aber ein spezieller Kernel verwendet welcher den Gradienten extrahiert. Ähnlich wie beim Smoothing gibt es auch beim Extrahieren der Gradienten verschiedene Methoden welche sich durch ihre Komplexität und der Qualität der Ergebnisse unterscheiden. In dieser Übung werden drei verschiedene Methoden behandelt:
- Rückwärts-Differenzen-Methode
- Zentral-Differenzen-Methode
- Sobel Methode
In den einzelnen Aufgaben sollen einzelne Berechnungen für das Extrahieren der Gradienten implementiert werden. Als Ergebnis erhalten wir ein neues Volumen welches in vier Komponenten den Datenwert (evtl. mit Smoothing) und die drei Vektorkomponenten des Gradienten enthält.
Im zweiten Schritt dieses Beispiels sollen die Gradientenwerte durch Glyphen abgebildet werden. Glyphen sind Symbole, deren visuelle Eigenschaften die gegebenen Daten repräsentieren. Konkret sollen an regelmäßigen Stellen im Volumen Super-Ellipsoide angezeigt werden. Die Gestalt, Orientierung und Farbe dieser Super-Ellipsoide erlaubt Rückschlüsse auf die Dichte, Stärke und Richtung des Änderungsfeldes im Volumen. Die folgenden Bilder zeigen, wie das für einen Schädel-Datensatz etwa aussehen könnte:
Plugin
Der Code zum Berechnen der Gradienten (TODO 1/2) befindet sich im Projekt plugin_editor_vislabfilterexercise, in den Dateien
EditorVislabFilterExcercise.h|cpp.
Der Code zum Rendern der Glyphen (restliche TODOs) befindet sich im Projekt plugin_renderer_vislabglyphexercise, in der Datei plugin_renderer_vislabglyphexercise.glsl.
Im C++ Code (RendererVislabGlyphExercise.cpp) werden an regelmäßigen Stellen im Volumen Positionen für Glyphen erzeugt. Diese Positionen der Glyphen werden an die Grafikkarte geschickt, an die Rendering-Pipeline gereicht und in Shaderprogrammen weiterverarbeitet. Das folgende Diagramm zeigt Details zur Pipeline, die aus einer Glyphposition einen fertigen, dem Volumendatensatz entsprechenden Glyphen erstellt:
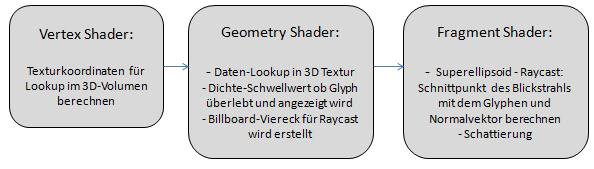
Jeder Glyph durchläuft folgende Schritte: Zunächst wird der Vertex-Shader einmal für jeden Glyphen ausgeführt, danach der Geometry-Shader ebenfalls einmal pro Glyph. Letzterer erzeugt an der Glyph-Position ein Billboard-Viereck, das durch den Rasterizer dann in viele Fragmente zerlegt wird. Der Fragment-Shader wird einmal für jedes Fragment (Pixel) der Billboard-Vierecke ausgeführt. Dabei wird für jedes Fragment der entsprechende Blickstrahl mit dem Superellipsoid geschnitten und aufgrund des erhaltenen Schnittpunkts und der Oberflächennormale die Beleuchtung pro Pixel durchgeführt. Fast alle Operationen in diesem Beispiel werden in Weltkoordinaten durchgeführt, einzig das Erstellen des Billboard-Vierecks geschieht im Viewspace.
Programmieraufgaben
| TODO | Beschreibung |
| 1 |
Gradient mittels Central-Differences
Hier sollen die Gradienten im Volumen mittels der Zentralen-Differenzen-Methode (central difference) berechnet werden. An der jetzigen Stelle für diese Berechnung im Code steht die Berechnung mittels der Rückwärts-Differenzen-Methode (backward difference). Diese soll so erweitert und verändert werden, dass anstatt der Rückwärts-Differenz die Zentral-Differenz für die Berechnung verwendet wird. Die Implementierung erfolgt in der Methode transform in der CentralDifferenceGradientFilter Klasse.
In der Übung ist das Volumen so definiert, dass jedes Voxel 4 Werte enthält. Mittels der Methode Get(int index) kann man auf einen dieser Werte zugreifen. Der Voxelwert mit dem Index 3 entält den (möglicherweise gefilterten) Datenwert. Die Voxelwerte mit den Indices von 0 bis 2 enthalten die drei verschiedenen Gradientenrichtungen (x, y und z). Diese sollen bei dieser Aufgabe neu berechnet werden.
Weitere Informationen zur Berechnung der Zentral-Differenz:
Allgemein (Wikipedia); Eindimensionaler und mehrdimensionaler Fall |
| 2 |
Gradient mittels Sobel-Filter
Als zweite Methode für die Gradientenberechnung soll ein Sobel-Kernel implementiert werden. Diese Aufgabe soll in der Methode transform der Klasse SobelGradientFilter gelöst werden.
Weitere Informationen über den Sobel Operator:
Sobel Operator (Wikipedia) |
| 3 |
Anwenden der Superellipsoid-Gleichung
Der Schnitt eines Blickstrahls mit dem Superellipsoid erfolgt nicht analytisch, sondern numerisch iterativ. Zunächst wird der Strahl mit der Bounding-Box des Ellipsoids geschnitten, ausgehend davon wird der genaue Schnittpunkt mit der Oberfläche iterativ gesucht. Dafür müssen Kandidatenlösungen (Punkte in 3D-Weltkoordinaten) immer wieder in die Gleichung des Superellipsoids eingesetzt werden. Die analytische Gleichung der für unsere Übung verwendeten Superellipsoide ist:
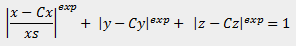 Cxyz ist der Mittelpunkt des Ellipsoids in Weltkoordinaten, xs ist einer der drei Radii des Super-Ellipsoids (Radius in x-Richtung). Die anderen beiden Radii sind 1.0, da wir nur Streckungen nach einer Richtung erlauben möchten. Somit liegen alle Punkte xyz auf dem Super-Ellipsoid, für die die obige implizite Darstellungsgleichung erfüllt ist. Setzt man Punkte ein, die innerhalb des Superellipsoids liegen, so wird die ausgewertete linke Seite der Gleichung kleiner sein als die rechte, für Punkte außerhalb des Ellipsoids ist die linke Seite größer.
Der Exponent exp definiert die Form des Superellipsoids. Die Klasse der mit dieser Gleichung darstellbaren Superellipsoide reicht von Kugeln (exp = 2, xs = 1) und Ellipsoiden (exp = 2, xs beliebig) bis hin zu spitzeren rautenförmigen Körpern (exp < 2) oder quaderartigen (exp > 2). Ein paar anschauliche Beispiele für den 2D-Fall (Superellipsen) gibt es hier.
In dieser Aufgabe ist die mathematische Grundlage des Glyph-Renderers zu schaffen. Für die Funktion evaluateSuperellipsoid() soll die Auswertung der linken Seite der obigen Gleichung für ein gegebenes Superellipsoid und einen gegebenen Punkt in 3D implementiert werden, und das Ergebnis als float-Wert zurückzugeben werden. Außerhalb der Funktion kann dann festgestellt werden, ob der Kandidatenpunkt der Iteration schon gut genug ist, um diesen zu akzeptieren. Nach der erfolgreichen Implementierung dieser Funktion sollten rote Glyphen als Kugeln dargestellt werden:
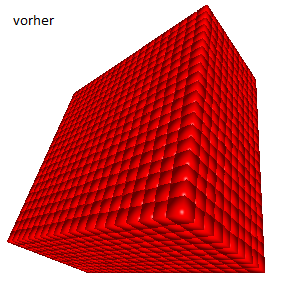
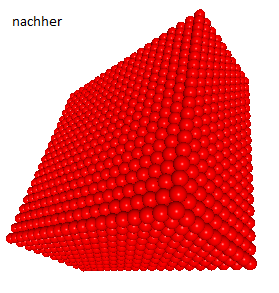 Der Grund, warum diese Aufgabe zuerst gelöst werden sollte, ist, dass man dann bereits Glyphen sieht und für die weiteren sechs Aufgaben wesentlich anschaulicheres Feedback bekommt.
|
| 4 |
Berechnung der Texturkoordinaten
Um an den Glyph-Positionen die zugrundeliegenden Daten des Volumens abfragen zu können, wird das Volumen in einer 3D-Textur gespeichert. Dabei handelt es sich um eine in Hardware interpolierbare Datenstruktur, in der in einem regelmäßigen Gitter mit normalisierten Koordinaten sämtliche vorhandenen Volumendaten abgelegt sind. Man kann sich die 3D-Textur als Funktion 3D -> 4D vorstellen, da jedem dreidimensionalen Punkt aus [0,1]x[0,1]x[0,1] ein vierdimensionales Tupel (GradientX, GradientY, GradientZ, Dichtewert) zugeordnet ist. Diese 3D-Textur befindet sich zum Zeitpunkt der Ausführung im Speicher der Grafikkarte und steht in Shaderprogrammen zur Verfügung.
In dieser Aufgabe sollen für jede Glyph-Position, die in den Vertex-Shader der Render-Pipeline gelangt, die 3D-Texturkoordinaten (je zwischen 0 und 1) dieser Position berechnet werden und für den späteren Lookup gespeichert werden. Dazu stehen folgende Parameter im Vertex-Shader zur Verfügung: fStartX, fStartY und fStartZ geben die minimalen Weltkoordinaten der Volumens-Boundingbox an, während fRangeX, fRangeY, fRangeZ die Ausdehnungen der Volumens-Boundingbox beschreiben. Mithilfe dieser Parameter soll nun ein direktes, lineares Mapping der Weltkoordinaten auf Texturkoordinaten durchgeführt werden (man kann davon ausgehen, dass die Bounding Box axis-aligned im Raum steht).
Ob die Texturkoordinaten richtig berechnet wurden, wird erst nach der Lösung der nächsten Aufgaben sichtbar.
|
| 5 |
Sample the Volume
Nachdem in der vorigen Aufgabe Texturkoordinaten für jeden Glyph berechnet wurden, können im nächsten Schritt für jeden Glyph die Daten aus dem Volumen gelesen werden. Die ersten drei Kanäle des Volumens (RGB) enthalten den Gradienten, der vierte Kanal (Alpha) den Dichtewert. Dazu ist der Befehl texture3D(Volumensresource, Texturkoordinaten) zu verwenden, der als vierdimensionalen Vektor die Werte des Volumens (3D-Gradient, Dichte) an der gefragten Stelle zurückliefert. Die erhaltenen Dichtewerte liegen zwischen 0 (minimale Dichte) und 1 (maximale Dichte), die Gradienten sind zum Auslesezeitpunkt nicht normalisiert und liegen koordinatenweise zwischen -1 und 1.
Ob die Implementierung des Lookups korrekt durchgeführt wurde, sieht man spätestens nach Fertigstellung der nächsten Aufgabe.
|
| 6 |
Glyph Threshold
Bislang wurden die Glyphen regelmäßig in einer gewissen Auflösung anzahlX*anzahlY*anzahlZ gezeichnet. Somit hätte man aber nie die Möglichkeit, innere Schichten im Volumen zu betrachten. Daher gibt es im grafischen User-Interface einen Parameter Glyph Threshold, der einen Schwellwert zwischen 0 und 1 angibt, den die Dichte des Volumens an einer Glyph-Position übersteigen muss, damit der Glyph angezeigt wird. Je höher der Threshold, desto mehr Glyphen verschwinden. Im Schädeldatensatz sind beispielsweise die äußeren Schichten eher wenig dicht (Luft, Haut, Gewebe), während der Schädelknochen oder die Zähne eine hohe Dichte aufweisen. Somit kann man durch Erhöhen des Schwellwerts die äußeren Schichten schrittweise wegblenden.
Momentan bewirken Veränderungen des GUI-Parameters Glyph Threshold noch nichts. In dieser Aufgabe soll diese Funktionalität im Geometry Shader implementiert werden. Der Schwellwert ist im Shader unter dem Namen fGlyphThreshold verfügbar, der Dichtewert des Glyphen steht in fVolumeIntensity. Sollte der Dichtewert nicht groß genug sein, so soll die Pipeline für diesen Glyphen frühzeitig mittels "return;" beendet werden, wodurch an dieser Stelle kein Glyph angezeigt wird.
Wenn die Implementierung korrekt durchgeführt wurde, sollten Veränderungen des "Glyph Threshold" sich auf die Anzahl der dargestellten Glyphen auswirken:
|
| 7 |
Visual Mapping - Teil 1
Zum jetztigen Zeitpunkt sehen alle Glyphen gleich aus, da die Superellipsoid-Parameter (Länglichkeit, Gestalt) standardmäßig immer auf xs = 1.0 (isotrop) und exp = 2.0 (kugelförmig) gesetzt werden. In dieser und den nächsten beiden Aufgabe sollen nun die Superellipsoid-Parameter entsprechend den Gradientenwerten gesetzt werden.
Zunächst soll das Mapping der Gradient Magnitude, also des Gradientenbetrags, auf die Länglichkeit des Glyphen durchgeführt werden. Homogene Regionen mit kleinem Gradienten sollen nahezu isotrope Glyphen erhalten, während mit steigendem Gradientenbetrag sich auch die Länglichkeit erhöhen soll. Für die Länglichkeit ist der Parameter xs verantwortlich.
Es soll ein lineares Mapping des Gradientenbetrags, gespeichert in fMagnitude, auf den Parameter xs wie vorgenommen werden:
fMagnitude = 0.0 --> xs = 1.0, also isotrop, nicht länglich
Je größer fMagnitude --> desto größer xs, also desto länglicher der Glyph Da die Gradientenbeträge so klein sind, dass man sie nur mit diesem Mapping kaum unterscheiden könnte, gibt es einen zusätzlichen Multiplikations-Faktor, der für das Mapping an die Gradient Magnitude multipliziert werden soll. Dieser
Parameter heißt im Shader fGradientScale und kann im GUI unter dem Namen Gradient Elongation Scale manipuliert werden.
Wenn die Implementierung korrekt durchgeführt wurde, sollten Glyphen in Regionen mit großem Gradienten je nach Wahl des GUI-Parameters Gradient Elongation Scale länglicher werden:
|
| 8 |
Visual Mapping - Teil 2
in der nächsten Aufgabe soll die Form der Glyphen durch das Mappen der Gradient Magnitude auf den Exponenten der Superellipsoide beeinflusst werden. Standardmäßig waren bislang alle Glyphen rund, da der Exponent immer auf den Default-Wert 2.0 gesetzt wurde.
Es soll ein lineares Mapping des Gradientenbetrags, gespeichert in fMagnitude, auf den Parameter exp wie folgt vorgenommen werden:
fMagnitude = 0.0 --> exp = 2.0, also rund
Je größer fMagnitude --> desto kleiner exp, also desto spitzer der Glyph Als untere Grenze soll jedoch exp = 1.0 gelten, da wir für diese Übung nur konvexe Formen darstellen möchten. Werte kleiner als 1.0 sollen also auf 1.0 "ge-clamped" werden.
Auch hier soll der zusätzliche Multiplikationsfaktor fGradientScale an den Gradientenbetrag multipliziert werden, damit kleinere Unterschiede besser erkennbar gemacht werden.
Anmerkung: Die korrekte Rotation der Glyphen, so dass sie in die Richtung des größten Anstiegs zeigen, ist übrigens schon implementiert und muss nicht bearbeitet werden.
Wenn die Implementierung korrekt durchgeführt wurde, sollten Glyphen in Regionen mit großem Gradienten je nach Wahl des GUI-Parameters Gradient Elongation Scale mehr oder weniger spitz dargestellt werden:
|
| 9 |
Visual Mapping - Teil 3
In der letzten Aufgabe soll nun der Dichtewert des Volumens auf die Farbe des Glyphen abgebildet werden. Hierzu soll exemplarisch folgendes Schema implementiert werden:
fVolumeIntensity = 0.0 --> Farbe rot RGB(1,0,0)
fVolumeIntensity = 1.0 --> Farbe grün RGB(0,1,0) Zwischen diesen beiden Werten soll linear interpoliert werden (z.B. bedeutet eine Dichte von 0.5 die Farbe gelb).
Wenn die Implementierung korrekt durchgeführt wurde, sollte die Farbe des Glyphen Aufschluss über den Dichtewert geben:
|
User Interface
Folgende GUI-Parameter stehen zur Verfügung:
| Name | Effekt | Zeigt Auswirkungen |
| Auto-Recompute | Wenn diese Option aktiviert ist wird eine Berechnung des gefilterten Volumens nach Änderung eines Parameters automatisch gestartet. Wenn es inaktiv ist, werden keine Berechnungen durchgeführt bis die Option wieder aktiviert wird. Der Fortschritt des Filterprozesses wird am unteren Rand in einer Progress-Bar dargestellt. | immer |
| Gradient Filter | Methode welche zur Berechnung der Gradienten verwendet wird. | ab TODO 1 |
| Smoothing Filter | Methode welche zum Smoothen der Daten verwendet wird. Bei None werden die Eingangsdaten gar nicht geglättet. | immer |
| Gaussian - Sigma | Die Standardabweichung für den Gauß-Filter. Diese Option ist nur aktiv wenn Gaussian als Smoothing-Methode ausgewählt ist. | immer |
| Bilateral - Sigma Domain | Standardabweichung für die räumliche Domäne beim bilateralen Filtern. | immer |
| Bilateral - Sigma Range | Standardabweichung für den Intensitätsbereich beim bilateralen Filtern. | immer |
| Glyph Density | Die Anzahl der Glyphen, die gerendert werden soll. Je größer dieser Wert, desto kleiner werden die Glyphen (damit es keine Überlappung gibt). | immer |
| Glyph Threshold | Der Schwellwert, den die Dichte übersteigen muss, damit ein Glyph angezeigt wird. | ab TODO 6 |
| Gradient Elongation Scale | Dieser Multiplikator gibt an, wie stark die Glyphen aufgrund des Gradientenbetrags in die Länge gezogen werden und ihre Form verändern. | ab TODO 7 |
| Shading Intensity | Wie stark die Beleuchtungssituation das Erscheinungsbild der Glpyhen beeinflusst (0 = nur Farben, 1 = maximales Shading). | immer |
| Diffuse Shading | Diffuse Komponente der Glyph-Oberflächenreflexion. | immer |
| Specular Shading | Spiegelnde Komponente der Glyph-Oberflächenreflexion. | immer |
| Specular Exponent | Glattheit des Glyph-Materials, beeinflusst die spiegelnde Reflexion. | immer |
Smoothing-Filter gehören wohl zu den beliebtesten Algorithmen in der Signalverarbeitung. Im Allgemeinen ist es ihr Ziel Rauschen zu unterdrücken und gleichzeitig das Signal so gut es geht zu erhalten. Das Filtern erfolgt in der Regel mittels einer Faltung des Signals mit einer Filter Funktion (auch Kernel genannt). Im Framework werden drei verschiedene Filterfunktionen verwendet:
- Average Filter
- Gauß Filter
- Bilateraler Filter
Hinweis
Falls Probleme mit der Performance auftreten:
- Glyph Density eher gering halten und den Threshold eher hoch.
- Weiter Hinauszoomen, sodass im Endeffekt wesentlich weniger Pixel berechnet werden müssen.
- Sollte beim Nachladen des Shaders der Grafikkartentreiber abstürzen (evtl. auf älteren Laptops), so deaktiviert man vor dem Nachladen das Renderingplugin kurz, lädt nach und aktiviert dann das Plugin wieder.






